GDC 2001: What Happend to My Colors !?!

Introduction

Anybody who has tried to display computer graphics on a TV knows that they look bad. Colors wash out, detail is lost, and the whole thing flickers. That's what happens when you're lucky. sometimes the graphics come out really badly.

While console game creators know that TVs do bad things to computer graphics, few of them are sure exactly what is happening. Sometimes "avoid bright red" or "don't use thin horizontal lines" is all they know.

This lack of understanding isn't surprising. NTSC (National Television Standards Committee) and PAL (European & South American Television Standards) encoding are quite complex, and the reasons they distort your graphics are not always obvious. Many of these distortions were barely visible when running low-resolution games, but the next generation of consoles means that every game will be running at high resolution, so we can't ignore these problems any longer.

The three main problems with displaying computer graphics on a TV are interlaced flicker, illegal colors, and reduced resolution. This article will explain what these problems are, and why they exist. Most of the concentrate will be on NTSC, but many of the issues also show up in PAL.

This article will briefly explain the important differences between NTSC and PAL, and will suggest ways to create your content so that it will suffer less when being displayed on a TV.

You've spent thousands of hours making your models, drawing your textures and optimizing your code. Don't let ignorance of the TV encoder ruin your masterpiece.

Interlace

An image which is rock solid on a computer monitor may flicker quite badly when displayed on a television. The computer image appears solid because the complete image is scanned out to the monitor sixty times a second or more. This is fast enough that the phosphors flickering on and off are perceived by the human mind as continuous light. However, on a television monitor, each individual line is only scanned out thirty times a second. Since the "fusion frequency", where a flashing light seems continuous, is generally around 50-60 flashes per second (Hz) we see flickering (Taylor 01).

What's actually happening on a television is that the electron beam scans over the picture tube sixty times a second, but only draws half of the lines. That is called one field. The next scan of the electron beam draws the other lines. Those two fields make up one 'frame' of video. This means that while each line is only drawn thirty times a second, the screen as a whole is drawn sixty times a second. This is called an interlaced display. The field rate is 60 Hz and the frame rate is 30 Hz. This can be confusing since the video game meaning of 'frame rate' is slightly different from the video meaning; however, usually it's clear which is meant.

The reason that TVs behave this way is because the NTSC was trying to get the best picture possible into a 6 MHz channel, and 6 MHz isn't enough bandwidth to transmit a full 525 line frame sixty times a second. They had to choose the best way to deal with this limitation.

One option would have been to increase the bandwidth available per channel. If they had doubled it to 12 MHz per channel then they would have avoided interlaced flicker entirely. However, that also would have cut the number of channels in half, something that the viewing public was unlikely to accept.

Another option would have been to display 525 lines at 30 frames per second. However, this frequency is so far below the fusion frequency that the flicker would have been completely unacceptable, which nobody would have tolerated.

Another option would be to display half as many lines, 262, at 60 frames per second. This would have produced flicker free television, but the vertical resolution would have been halved.

It is worth noting that the movie industry deals with this same 'bandwidth' problem in a very different way. Since film is expensive, movies are shot at 24 frames per second. However, if they simply played them back at 24 frames per second the flicker would be unbearable. Instead, they display each frame twice, to give a 48 frame per second flicker rate. In a darkened theater, that's enough to seem continuous. It would seem that the same effect could be obtained by displaying each frame for a full twenty-fourth of a second, instead of flashing it twice, but in fact this interferes with the perception of movement.

The reason the television industry didn't adopt the same solution as the movie industry is simple, no frame buffers. Television is a real-time medium, with the phosphors on the television lit up as the information streams in. In 1941, there was no way of buffering up a frame and displaying it twice. This option has only become economically feasible very recently. The other reason that displaying a full frame buffer twice is not used, even with HDTV, is that 60 fields per second gives noticeably smoother motion than 30 frames per second.

Another tempting option that couldn't be used was phosphors that would glow longer after the electron beam left. This method would have introduced two problems. One problem would be that the sense of motion would actually be reduced, which is what occurs if you display a movie frame for a full twenty-fourth of a second. The other problem is that it is impossible to make phosphors that fade out instantly after precisely one thirtieth of a second, and the gradual decay of the brightness would produce substantial blurring of motion.

Therefore, as much as I dislike interlace, I have to agree that it was the right choice.

The good news is that the flicker isn't really that bad. Television shows and movies seem to flicker significantly less than computer graphics. If we can learn what the video professionals do right that we so often do wrong we can improve our results.

The bad news is that the trick is to avoid fine vertical detail. The worst-case flicker happens if you have a single-pixel high, horizontal white line on a dark background. In such a case, the fact that the monitor is being refreshed 60 times a second is irrelevant. Your only visible graphics are being refreshed 30 times a second, and that's nowhere near enough. You can also get strong flicker if you have a large bright area with a large dark area below it with a sudden transition, because on the transition area you are effectively displaying at 30 Hz.

The key is to avoid the sudden transitions. If you have a scan line of 50% gray between your bright white and your black then the flicker will be dramatically reduced, because when the white line is not being displayed, the gray line overlaps a bit and stops the image from fading away to black (Schmandt 87).

The best thing to do may be to vertically blur all of your static graphics including menu screens and some texture maps in order to soften sudden transitions in brightness. Alternately, most of the new generation of consoles will do this for you. As the image buffer is sent to the television they will carefully average together two to five adjacent scan lines to eliminate transitions that are too fast. While turning on an option to blur your graphics seems like an odd way to improve your image quality, even a desecration of your carefully drawn art, it really is the right thing to do. Maybe if we call it vertical filtering instead of vertical blurring it will sound more scientific and reasonable. Let's do that.

As an example, the Conexant CX25870/871 video encoder does five-line horizontal and vertical filtering. In order to reduce flicker without excessive blurring it adjusts the filter amounts on a pixel-by-pixel basis based on how flicker prone the imagery is (Conexant 00).

The reason that television programs don't flicker objectionably is because reality doesn't usually have high contrast, high-frequency information, and because some video cameras do vertical filtering. The sample height for each scan line in a video camera can be almost twice the height of a scan line (Schmandt 87), thus pulling in a bit of information from adjacent lines. Therefore, even if there is a thin horizontal line in a scene, it will be spread out enough to reduce the flicker. This is further justification for why we should do exactly the same thing with our graphics.

One important thing to understand about vertical filtering is that it is best done on a full frame. If you are running your rendering loop at 60 Hz and only rendering a half height image then vertical filtering will not work as well - the line that is adjacent in memory will be too far away in screen space. If vertical filtering is to work properly, it has to have the other field of data so that it can filter it in. This can be a problem on consoles where fill rate or frame buffer memory restrictions make it tempting to render just a half height image. If fill rate is the limiting factor then you can do field rendering at 60 Hz but keep the alternate field around and use it for vertical filtering. If frame buffer memory is the limiting factor, you may need to use a 16-bit frame buffer to make room for a full frame.

Just because you are rendering a full height frame doesn't mean that you have to display this frame at 30 frames per second. For most games the sense of motion is substantially improved at 60 frames per second, so you should render a full height frame, 60 times per second, then get the video hardware to filter it down to a single field on the way to the TV. This does mean that you have to render an awful lot of pixels per second, but that's what the beefed up graphics chips are for!

Giving up some of the 480 lines of resolution is hard to do. However, it can be helpful to realize that the reason the vertical filtering works is because adjacent scan lines overlap a bit. Therefore, you never really had 480 lines of resolution anyway.

The good news is that, for some purposes, you can simulate much higher vertical resolution. If you draw a gray line instead of a white line then it will be perceived as being thinner. This doesn't help if you want a lot of thin lines close together, but it is useful if you want a line that is half a pixel high, or a pixel and a half high.

The next time you're cursing the NTSC for inflicting interlace on you it's worth noting that when they designed the NTSC standard, the flicker wasn't as bad. The phosphors of the standard were much dimmer than the phosphors that are actually used today, and today's brighter phosphors, together with brighter viewing conditions, make us more flicker sensitive.

If you think making video games for an interlaced medium is annoying, you should try creating a video editing system. Video game authors have the luxury of synthesizing a full frame of graphics sixty times a second, something video-editing systems can't do. This makes for some interesting problems when you rotate live video on screen. The missing lines are suddenly needed and they have to be somehow extrapolated from adjacent fields.

If you are used to making video games that run at non-interlaced resolutions, like 320x240, then going to 640x480 does not mean that your vertical resolution has doubled. It has increased a bit, and that's good, but you need to understand from the beginning that if you create 480 lines of detail, it won't be visible. The actual vertical resolution is somewhere between 240 and 480, which means that small details necessarily cover around one and a half scan lines.

If it's any consolation, NTSC resolution could have been lower. It wasn't until the very last meeting of the first NTSC that the resolution was raised from 441 lines to 525 lines.

So remember, if your target console has an option to vertically filter your images, enable it, and render full frames. If it doesn't have such an option, do it yourself before putting the art in the game. There's no point in putting in beautiful vertical detail if it will be invisible and will give your customers a headache.

Illegal Colors

RGB is the color space of our retina, of picture tubes, of still cameras and of motion cameras. RGB is the color space of ray tracing and other simulations of the interactions between light and objects. Why? Because our eyes have red, green and blue detectors. Therefore, RGB color space accurately models the way that our retina detects light. In addition, if you work in RGB space you can take the contributions of two lights, add them together, and get a meaningful result.

However, RGB is not the color space of our visual cortex. Somewhere between our retina and where we perceive color, another color space becomes a better representation of how our mind sees color. Although artists find it convenient to work with hue and saturation, our mind seems to perceive color roughly as a combination of brightness and two axes of color information. YUV and YIQ color space attempt to capture this color space.

Y stands for luminance (brightness) and it is calculated as:

Y = .299R'+.587G'+.114B'

The weightings are based on our eye's sensitivity to the different primaries. The prime signals after R, G and B indicate that these are gamma corrected RGB values, which I'll discuss later. U and V represent no numerical value per se. They're just two adjacent letters of the alphabet and are calculated as:

U =0.492(B'-Y)
V =0.877(R'-Y)

This gives us two numbers that are zero when we have gray and can hold all of the color information of an RGB color. You can think of the Y coordinate of YUV as measuring how far along the gray diagonal of the RGB color cube to go. The U and V coordinates then specify how far from gray to go, and in which direction.

However the NTSC designers didn't choose YUV as their color space, they chose a closely related color space called YIQ. YIQ is simply a 33-degree rotation of U and V so that the color coordinates line up slightly better with the way we see color. Thus, the formulae for I and Q are:

I =V cos(33)-U sin(33)=0.736(R'-Y)-0.258(B'-Y)
Q =V sin(33)+U cos(33)=0.478(R'-Y)-0.413(B'-Y)

U and V don't stand for anything, but what about I and Q? You probably shouldn't ask. Since YIQ was first used by NTSC television, its name reflects the method used to squeeze the I and Q signals together into one signal. The method used is called "quadrature modulation" (a method also used in modems). Thus, I stands for "in-phase" and Q stands for "quadrature."

After I and Q are squeezed together into one signal, they are added to the Y component to produce a composite signal resulting in Y, I and Q all being mixed together on a single wire. It's very complicated to explain how and why this signal can usually be pulled apart into its components again by a TV, and Jim Blinn's article on NTSC spends a lot of time explaining why this works (Blinn 98). However all this high powered math to explain how to extract YIQ from a composite signal hides the fact that going in the other direction, creating a composite signal from YIQ, is actually trivial.

Since we are starting with an RGB image we first convert from RGB to YIQ. Then we need to filter Y, I, and Q to remove the high frequencies, which is discussed in more detail in the following section. Then, I + Q are combined using quadrature modulation to make chroma, the color information. The formula for this is simply (Jack 98):

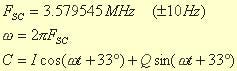
3.579545 MHz is the color carrier frequency, carefully chosen to go through precisely 227.5 cycles for each horizontal line, and t is time. The effect of this formula is to take two copies of the color carrier, one offset by ninety degrees, and multiply them by I and Q. When they are added together the result is another sine wave at the color carrier frequency. The amplitude of this resultant sine wave stores the saturation of the color, measuring how pure it is. The offset of the sine wave in t, known as the phase, stores the hue of the color.

Finally, C is added to Y, and you've got your composite signal:

Composite =Y+C

When the signal gets to your TV, your TV has to convert it back to RGB, because televisions are fundamentally RGB devices. If you use enough precision and do careful rounding then converting from YIQ and back to RGB is lossless. So why do we care about this conversion?

To understand why we care we need to look a little bit more at the quadrature encoding that adds I and Q together to make C. As I mentioned above, quadrature modulation gives us a sine wave. The amplitude of this sine wave is:

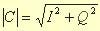
Remember that this sine wave is added to the Y signal so the Y + C signal will swing higher and lower than Y by itself. It will go as high as Y + |C| and as low as Y - |C|. A little experimentation will show that some combinations of red, green, and blue will create large swings. If R', G' and B' go from 0.0 to 1.0 then the maximum value for Y + |C| is 1.333 and the minimum value for Y - |C| is -0.333. Pure red and pure green will cause the signal to swing down to -0.333 and pure cyan (blue and green) and pure yellow (red and green) will cause it to swing as high as 1.333. Meanwhile, pure white only goes up to 1.0, and pure black sits at 0.0. In general, highly saturated colors, colors with very little white in them, will cause high voltage swings.

It may seem odd that yellow and cyan cause higher signals than pure white, but this actually does make sense. The average signal for pure yellow is just 0.886, but the color carrier, C, swings up 0.447 and down 0.447 from 0.439 to 1.333. It is this wild swinging of the color carrier that tells the TV to display yellow. Meanwhile, pure white gives a steady 1.0 signal.

NTSC Composite Waveform for Pure Yellow

Notice how the composite signal for yellow goes up quite high. In this image the signal would have gone up to 1.333 but it was clamped at 1.20. The high amplitude of the signal indicates a highly saturated color.

NTSC Composite Waveform for White

The composite waveform for white is quite boring. It's just a straight line. That shows that it has zero saturation, or no color. Also note that while the yellow signal goes much higher than white does, the average height of the white signal is higher than the average height of the yellow signal. This indicates that white is a brighter color, and it has greater luminance.

NTSC Composite Waveform for Pure Red

By now, I'm sure that you recognize this waveform as being a highly saturated signal with relatively low luminance. This means it must be red or blue. The phase of the waveform makes it obvious that it is red. Okay, maybe not so obvious, but the sine wave is clearly shifted to the right a bit compared to yellow, thus indicating a non-yellow hue. Saturated colors that use two primaries tend to go off the top of the graph, because they are naturally brighter. Saturated colors that have a lot of just one primary tend to go off the bottom of the graph. This signal went down to -0.333, but was clamped at -0.20.

The problem is, the NTSC signal isn't allowed to go up 33% higher than white. That would have destroyed backwards compatibility with the millions of monochrome sets in use when color NTSC was designed. Scaling all of the signals down would have allowed pure yellow to be transmitted, but it would have reduced the precision for other colors, and would have made color TV signals dim when compared with monochrome signals. So, the designers of the NTSC color system compromised. Pure yellow and cyan are pretty rare in nature, so they specified that the signal could go 20% above white and 20% below black. In other words, they said that you are not allowed to broadcast certain highly saturated colors.

In some cases, it's not even a matter of not being allowed to; it's actually physically impossible! On broadcast TV, the voltage encoding for 20% higher-than-white is zero volts (high voltage is used for black). So, pure yellow would require negative voltage, an impossible voltage to broadcast. Clamping the signal causes all the same problems you get with clipping when recording loud sounds. The signal usually gets terribly distorted, and it's not worth doing.

We're not trying to broadcast our graphics, so our bright yellows and pure reds might actually make it to the television, but TVs were never designed to handle those signals so it is unlikely that they will handle them well. These highly saturated colors tend to throb and pulsate. If the signal is clipped to the broadcast limits, then the signal will be distorted and nearby pixels may show unpredictable problems. Highly saturated colors also increase problems with chroma and luminance cross talk by making it harder to cleanly separate chroma and luminance.

The worst-case RGB combinations, known as "hot" or "illegal" colors are:

1, 1, 0 - yellow
0, 1, 1 - cyan
1, 0, 0 - red
0, 0, 1 - blue

You can fix red by reducing the luminance, but you have to reduce it to 0.60 to get it just barely into legal range. This changes the color a lot.

Alternately you can fix red by reducing the saturation, while holding the luminance constant. This means subtracting 0.15 from the red and adding about 0.06 to blue and green. This changes the color much less.

Finally, you can fix red by just adding 0.10 to green and blue. There is no mathematical justification for this. Instead, you're actually increasing the brightness, but it looks very good. It fixes the problem because increasing the green and blue lowers the saturation more than it increases the brightness. Similar fixes work for the other problematic colors.

The saturation fix seems to be the best programmatic solution, but an artist's touch can give even better results.

The following code is a simple function for detecting illegal NTSC colors:

#include
#include

const double pi = 3.14159265358979323846;
const double cos33 = cos(33 * pi / 180);
const double sin33 = sin(33 * pi / 180);

// Specify the maximum amount you are willing to go
// above 1.0 and below 0.0. This should be set no
// higher than 0.2. 0.1 may produce better results.
// This value assumes RGB values from 0.0 to 1.0.
const double k_maxExcursion = 0.2;

// Returns zero if all is well. If the signal will go too high it returns how
// high it will go. If the signal will go too low it returns how low it
// will go - a negative number.
// It is not possible for the composite signal to simultaneously
// go off the top and bottom of the chart.
// This code is non-optimized, for clarity.
double CalcOverheatAmount(double r, double g, double b)
{
assert(r >= 0.0 && r <= 1.0);
assert(g >= 0.0 && g <= 1.0);
assert(b >= 0.0 && b <= 1.0);
// Convert from RGB to YUV space.
double y = .299 * r + .587 * g + .114 * b;
double u = 0.492 * (b - y);
double v = 0.877 * (r - y);

// Convert from YUV to YIQ space. This could be combined with
// the RGB to YIQ conversion for better performance.
double i = cos33 * v - sin33 * u;
double q = sin33 * v + cos33 * u;

// Calculate the amplitude of the chroma signal.
double c = sqrt(i * i + q * q);
// See if the composite signal will go too high or too low.
double maxComposite = y + c;
double minComposite = y - c;
if (maxComposite > 1.0 + k_maxExcursion)
return maxComposite;
if (minComposite < -k_maxExcursion)
return minComposite;
return 0;
}

Once you have identified a hot color there are two easy programmatic ways to fix it - reduce the luminance, or reduce the saturation. Reducing the luminance is easy, just multiply R', G' and B' by the desired reduction ratio. Reducing chrominance is only slightly harder. You need to convert to YIQ (although YUV actually works just as well) then scale I and Q or U and V and then convert back to RGB (Martindale 91). The code snippets below will calculate and use the appropriate reduction factors to get the colors exactly into legal range.

// This epsilon value is necessary because the standard color space conversion
// factors are only accurate to three decimal places.
const double k_epsilon = 0.001;

void FixAmplitude(double& r, double& g, double& b)
{
// maxComposite is slightly misnamed - it may be min or max.
double maxComposite = CalcOverheatAmount(r, g, b);
if (maxComposite != 0.0)
{
double coolant;
if (maxComposite > 0)
{
// Calculate the ratio between our maximum composite
// signal level and our maximum allowed level.
coolant = (1.0 + k_maxExcursion - k_epsilon) / maxComposite;
}
else
{
// Calculate the ratio between our minimum composite
// signal level and our minimum allowed level.
coolant = (k_maxExcursion - k_epsilon) / -maxComposite;
}
// Scale R, G and B down. This will move the composite signal
// proportionally closer to zero.
r *= coolant;
g *= coolant;
b *= coolant;
}
}

void FixSaturation(double& r, double& g, double& b)
{
// maxComposite is slightly misnamed - it may be min
// composite or maxComposite.
double maxComposite = CalcOverheatAmount(r, g, b);
if (maxComposite != 0.0)
{
// Convert into YIQ space, and convert c, the amplitude
// of the chroma component.
DoubleYIQ YIQ = DoubleRGB(r, g, b).toYIQ();
double c = sqrt(YIQ.i * YIQ.i + YIQ.q * YIQ.q);
double coolant;
// Calculate the ratio between the maximum chroma range allowed
// and the current chroma range.
if (maxComposite > 0)
{
// The maximum chroma range is the maximum composite value
// minus the luminance.
coolant = (1.0 + k_maxExcursion - k_epsilon - YIQ.y) / c;
}
else
{
// The maximum chroma range is the luminance minus the
// minimum composite value.
coolant = (YIQ.y - -k_maxExcursion - k_epsilon) / c;
}
// Scale I and Q down, thus scaling chroma down and reducing the
// saturation proportionally.
YIQ.i *= coolant;
YIQ.q *= coolant;
DoubleRGB RGB = YIQ.toRGB();
r = RGB.r;
g = RGB.g;
b = RGB.b;
}
}

Complete code is available on my web site. Included is a sample app that lets you interactively adjust RGB and HSV (hue, saturation, value) values while viewing the corresponding composite waveform. The program also lets you invoke the FixAmplitude() and FixSaturation() functions, to compare their results.

It's worth noting that there are also YIQ colors that represent RGB colors outside of the unit RGB cube. Video editors who do some of their work in YIQ or YUV need to deal with this, but we don't have to.

Overall, it's best to avoid using colors that will go out of range. Many image-editing programs have a tool that will find and fix 'illegal' or 'hot' NTSC colors. If you want more control, a tool that finds and fixes illegal colors is available on my web site. One advantage of a home grown tool is that you can decide, based on your target console and artistic sensibilities, how close to the maximum you want to go, and how to fix colors when you go out of range.

I mentioned at the beginning that the prime symbols that I try to remember to use on R', G' and B' indicate that these calculations are supposed to be done on gamma corrected RGB values. Therefore, it seems reasonable to ask whether our RGB values are gamma corrected. The good news is, they usually are, and when they're not, it usually doesn't matter. Alternatively, to put it more brutally, the game industry has successfully ignored gamma for this long, why change now?

The reason our images are mostly gamma corrected is that TVs and computer monitors naturally do a translation from gamma corrected RGB to linear light (Poynton 98). This is a good thing because it means that the available RGB values are more evenly spread out according to what our eyes can see. Since we create our texture maps and RGB values by making them look good on a monitor, they are naturally gamma corrected (although some adjustments are needed because monitors and televisions may have different gamma values).

However, if we do a lot of alpha blending and antialiasing then we are doing non-gamma corrected pixel math. If we do a 50% blend between a white pixel and a black pixel, presumably we want the result to be a pixel that represents half the light density, or half as many photons per second. However, the answer that we typically get is 127, which does not represent half as many photons, because the frame buffer values don't represent linear light. The correct answer that you can verify by playing around with various sized black white dither patterns and comparing them to various grays, is typically around a 186 gray. It's not a huge error, and unless graphics hardware starts supporting gamma corrected alpha blending, there is nothing we can do.

Resolution Limitations

The nice thing about the YUV color space is that our eyes can see much finer brightness detail than color detail, so U and V can be stored at a lower resolution than Y. The JPEG format makes use of this initially converting from RGB to YUV and then throw away three quarters of the U and V information, half in each direction. When it does this, JPEG gets a guaranteed 50% compression before it even starts doing its discrete cosine transforms.

The YIQ and YUV color spaces are virtually identical. YIQ is just a thirty-three degree rotation of the UV axes. In fact, you can generate NTSC video from YUV quite easily since the hue ends up in the phase of the color carrier, and since YIQ is just a thirty-three degree hue rotation from YUV, you just need to offset the chroma waveform by thirty-three degrees to compensate.

So why does NTSC carefully specify the YIQ color space if YUV would have been identical? The reason is that the sensitivity of your eyes to color detail is also variable. You can see more detail in the orange-cyan color direction, the I channel of YIQ, than you can in the green-purple color direction in the Q channel. Therefore, you can go one step beyond the UV decimation of JPEG and store Q at a lower data rate than I. This would not have worked well with YUV.

Backwards compatibility is another reason why YIQ was a good choice for the NTSC color space. The first NTSC in March 1941 created the standard for monochrome television. The second NTSC issued the color standards in 1953, by which time there were tens of millions of monochrome TVs, and many television stations. To be successful, as opposed to CBS's failed field sequential color system, the new color system had to be backwards compatible. Owners of color TV sets would want to watch monochrome broadcasts, while color broadcasts needed to be visible on monochrome TV sets. That they managed to make this work at all is simply amazing.

YIQ works well for backwards compatibility because the Y signal is equivalent to the monochrome signal. By carefully encoding the color information of I and Q, so that monochrome receivers would ignore it, the NTSC managed the necessary backwards compatibility.

This magic trick was only possible because our eyes are less sensitive to color detail. The I and Q signals can be transmitted at a much lower rate without our eyes noticing the relative lack of color information. This makes it easier to squeeze I and Q into an already crowded wire. Y was given a bandwidth of 4.2 MHz, which Nyquist tells us is equivalent to roughly 8.4 million samples per second. When I and Q were added, I was given 1.3 MHz of bandwidth, and Q a paltry 0.6 MHz. Thus, the total bandwidth was increased by less than 50%.

The lower frequencies of I and Q were justified by studies of the human visual system, which showed less sensitivity to detail in those areas. However even the 8.4 million 'samples' per second of the luminance channel is not very high. If we work out the data rate in a 640 by 480 frame buffer displayed 30 times a second (or, equivalently, a 640 by 240 frame buffer displayed 60 times a second), we get a figure of 9,216,000 pixels per second. That wouldn't be so bad except that NTSC is a real-time standard. A television spends about 25% of its time doing vertical blanking and horizontal blanking. During this time, when the electron beam is stabilizing and preparing to draw, the 4.2 MHz signal is essentially wasted. So, we really only have about 6.3 million samples with which to display over 9 million pixels per second. This means that if you put really fine detail into your screens, perhaps thin vertical lines or small text, then it is impossible for the television to display it.

Although the luminance signal is allowed to go as high as 4.2 MHz, it can encounter problems long before it gets there. Because the color information is stored at 3.579545 MHz, you can't also store luminance at that frequency. The color frequency was chosen to be a rare frequency for luminance, but if you accidentally generate it then either the encoder will notch filter it out, or the TV will interpret it as color!

If you do put in fine horizontal detail then the best thing that can happen is it may be filtered away, rendering your text unreadable. The alternative is actually worse. If the high frequency detail isn't filtered out then your television may have trouble dealing with the signal. If you are connected to the TV with an RF (radio frequency) connector then the high frequencies will show up in the sound. With a composite connector, they may show up in the chroma information, giving you spurious colors.

Similar problems happen with the I and Q information. Quadrature modulation is basically equivalent to interleaving the I and Q signals into one signal (Blinn 98). I and Q can only be separated at the other end only if their frequencies are each less than half of the color carrier frequency of 3.58 MHz. The original bandwidth limitations of 1.3 and 0.6 MHz for I and Q were chosen to respect this limitation, and because Q is less important. Since 1953 filters have gotten a lot better so that I and Q can now both be transmitted at 1.3 MHz.

Still, 1.3 MHz is not very fast. Color changes in NTSC happen more than three times slower than luminance changes. If you have thin stripes of pure magenta on a 70% green background then the Y value will remain constant, but I and Q will oscillate madly. If that oscillation is filtered out, your thin lines disappear. If it isn't, then the color information will show up as inappropriate brightness information. Luckily, the worst cases tend to be rare such as purple text on a green background, which is not something that people do intentionally.

There are excellent video encoders available which do a great job of filtering out the abusive graphics we throw at them. However filtering is not perfect, and the more you push the limits, the more likely you are to run into troubles. Even if the television encoder in your target console filters your high frequencies down to exactly the proper limits, that's a small consolation if many of your customers hook up TVs that handle the boundary cases badly.

I received the inspiration for this article was when I was staring at a section of one of our console game menu screens displayed on a TV. The area I was staring at appeared to be solid green, yet it was flickering far worse than any interlaced flicker I've ever seen. It turns out that the source image wasn't solid green. The color was changing quite frequently between black and green. Even though the color changes were not showing up at all, they were getting to the TV in some distorted form, and causing serious problems. Since the color carrier takes four fields to repeat itself (227.5 cycles per line * 262.5 lines per field means 59718.75 cycles per field) in the worst case this can cause artifacts which repeat every four fields, or fifteen times a second, and flicker twice as bad as interlaced flicker.

The solution was to remove the fine detail. Since it wasn't visible on the TV anyway, the only effect was that the image stabilized. This served as a dramatic lesson in the importance of avoiding high frequency images.

It is incredibly difficult for a television to separate the chroma information from the luminance information. Comb filters help, but they come with their own set of problems. Probably the most common symptom of poor chroma-luminance separation is called chroma crawl. This happens when high-frequency chroma information is decoded as luminance. This causes tiny dots along vertical edges. These dots appear to crawl up the edge as the four-field NTSC cycle puts the excess chroma in a different place for each field.

The underlying problems with high horizontal frequencies are quite different from those for interlaced flicker, but the solutions are very similar. Avoid high frequencies, and consider filtering your images horizontally to avoid them. Using antialiased fonts and dimmed lines to represent thin lines can dramatically improve your effective resolution.

The most important thing to do is antialiased rendering. The highest frequencies that you will encounter in your game will be on edges that aren't antialiased and on distant textures that aren't mip-mapped. Modern console hardware is fast enough to avoid these problems, and it is important to do so. Occasionally, you will hear people claim that the blurry display of television will hide aliased graphics and other glitches. This is not true. Aliased edges are the biggest causes of chroma crawl and interlaced flicker, and distant textures that aren't mip-mapped cause such random texture lookup that no amount of blurring can cover it.

Learn the signs of excessively high frequencies. If a still image is flickering, try filtering vertically to see if interlace is the problem. If the flicker remains, or if you see color in monochrome areas or chroma crawl along sharp edges, try filtering it horizontally. With a little bit of effort, you can translate an image to YIQ, filter Y, I and Q separately, and then translate it back. This lets you find out exactly where the problem is.

What About PAL and HDTV?

PAL was designed in 1967, fourteen years after NTSC, and was not backwards compatible with the previous monochrome format. That gives PAL a few advantages over NTSC. However, it had to deal with the same physical bandwidth limitations that restrict NTSC so PAL still has quirks and limitations.

PAL uses the YUV color space rather than YIQ and it supports the full range, so that over-saturated colors are not a problem. PAL also has more bandwidth devoted to the composite signal, allowing higher horizontal resolution, and has 625 lines instead of the 525 lines of NTSC.

On the downside, PAL has a lower refresh rate of 50 Hz interlaced, which makes flickering worse. The color-encoding scheme used by PAL works best if the color information from adjacent lines is blurred together by the TV, thus, lowering vertical color resolution.

PAL's greatest advantage is probably the great number of TVs that have high quality SCART connections, allowing all of the problems except for interlaced flicker to be avoided when playing video games.

HDTV is great. At the lowest resolution of 720x480, you actually get to virtually see all of those pixels. In addition, the 720x480 resolution is a progressive scan resolution with no interlaced flicker. HDTV's are rare now, but the new generation of consoles just might be the killer app to push consumers to get them.

If things had worked out differently, we could have had a radically different set of TV problems. In 1950, the FCC approved a color television system designed by CBS, with the first broadcast happening June 25, 1951. However, virtually nobody saw it because only a few dozen of the twelve million television sets in America could receive color. The CBS standard was designed to work with TVs featuring a spinning filter wheel. One hundred and forty-four fields per second were broadcast displaying red, green, and blue sequentially. Thus a complete field could be displayed 48 times a second, and a complete frame 24 times a second (Reitan 97).

If the CBS standard hadn't died then we would have a television standard that was much more compatible with film - it has the same frame rate. It would have avoided the high-pitched 15KHz hum of NTSC. However, we would have had a pair of spinning wheels inside our TVs rotating at 1440 rpm. Finally, we would have just had 405 vertical lines instead of 525.

It Doesn't Have to be This Way

Many of the limitations of NTSC come from the need to transmit a backwards-compatible signal through the air (or through conventional cable with the frequency limitations being the same). However, there are an increasing number of consumers who aren't using their TVs in this way. If you are playing console video games, web browsing on your TV, or watching digital cable or digital satellite TV then there is an RGB frame buffer located less than ten feet from your TV. Why on earth are we squeezing that perfect RGB frame buffer into an archaic 6MHz signal so that we can carry it across our living room! S-Video is a big step towards avoiding the pointless encoding and decoding by keeping the luminance and chrominance signals separate. However, even S-Video is still limiting the bandwidth of the I and Q signals.

If console video games, digital cable boxes, and digital satellite boxes had RGB output jacks and if TVs started more commonly having RGB input, then most of these problems, excluding interlaced flicker, would go away. There have been many reasons to support direct RGB connections in the living room for a number of years now, but a lack of consumer demand or a lack of industry support has left us with composite connections as the standard.

What Can Game Players do About These Problems?

As a consumer, there are quite a few things you can do to improve the video game images and other graphics displayed on your TV. The basic trick is to avoid putting too many signals on a single wire.

An RF connection to your TV is the worst. RF means that Y, I and Q are combined with the sound channel on a single wire, and there are many ways they can interfere with each other.

The next best thing is a composite connection, which at least keeps the sound separate.

S-Video keeps Y and C separate, thus avoiding chroma crawl and allowing the Y signal to have higher frequencies. Since separating Y and C is the hardest task for a TV, S-Video produces the largest jump in video quality.

Finally, component video such as YUV or RGB keeps each signal on a separate wire and should allow the full resolution to be displayed.

If you're in Europe then you can use a SCART connector for RGB input, and they are common enough that you can even assume that a lot of your customers will use them.

What Can Game Authors do About These Problems?

Fancy connectors are great for your own personal setup, but don't make the mistake of assuming that your customers will be plugging an RGB connector into their home theatre. The most common connection in North America is composite so be sure to test your game with it.

Sophisticated RGB encoders can insulate you from some of the problems of NTSC, but they won't let you exceed its fundamental limitations.

Avoid thin horizontal lines. Horizontal lines typically cause flickering. If there is a vertical filtering option, use it. Doing this properly requires that you render a full frame, even if you are running at 60hz.

Menu screens with too much detail frequently cause the worst flickering. They are also the easiest to fix, since you are explicitly creating each pixel. Making full use of the available resolution means creating detail that has a fractional pixel width.

Use low contrast lines to simulate thin lines, and use antialiased fonts to allow greater detail.

If you find that your graphics are displaying poorly then write a tool to filter your screen shots appropriately in Y, I and Q to see how much you are exceeding the limits. Refer to my web site for sample codes. If necessary, you can pre-filter your texture maps. Remember that brightness-detail smaller than one and a half pixels wide can't be displayed, and color-detail smaller than five pixels wide will also be filtered out.

Check for illegal colors.

Antialiasing matters a lot. Texture filtering and mip-mapping help within a particular texture map, but do not help at texture map or object boundaries. Full scene antialiasing will not only remove jaggies, it will also help avoid chroma crawl and other artifacts.

Don't just test on one TV - and certainly don't just test on one really expensive TV with a comb filter or an S-Video connector. This will give you an inaccurate view of what your game will look like to most people. Test on what your target market uses. It can make a big difference.

References
Blinn, James, NTSC: Nice Technology, Super Color, Dirty Pixels, Morgan Kaufmann Publishers, Inc., 137-153

Conexant, Adaptive Flicker Filter, Video Encoder, CX25870/871 - 100431_pb.pdf

Jack, Keith, Video Demystified, Second Edition, LLH Technology Publishing

Martindale, David and Paeth, Alan W., "Television Color Encoding and "Hot" Broadcast Colors", Graphics Gems II, Academic Press, Inc., 147-158

Poynton, Charles, Gamma FAQ

Reitan, Ed, CBS Field Sequential Color System

Schmandt, Christopher, "Color Text Display in Video Media", Color and the Computer, Academic Press, Inc.

Taylor, Jim, DVD Demystified, Second Edition, McGraw Hill

______________________________________________________