Advanced Collision Detection Techniques

Author: by Nick Bobic

Since the advent of computer games, programmers have continually devised ways to simulate the world more precisely. Pong, for instance, featured a moving square (a ball) and two paddles. Players had to move the paddles to an appropriate position at an appropriate time, thus rebounding the ball toward the opponent and away from the player. The root of this basic operation is primitive(by today’s standards) collision detection. Today’s games are much more advanced than Pong, and most are based in 3D. Collision detection in 3D is many magnitudes more difficult to implement than a simple 2D Pong game. The experience of playing some of the early flight simulators illustrated how bad collision detection can ruin a game. Flying through a mountain peak and surviving isn’t very realistic. Even some recent games have exhibited collision problems. Many game players have been disappointed by the sight of their favorite heroes or heroines with parts of their bodies inside rigid walls. Even worse, many players have had the experience of being hit by a rocket or bullet that was “not even close” to them. Because today’s players demand increasing levels of realism, we developers will have to do some hard thinking in order to approximate the real world in our game worlds as closely as possible.

This article will assume a basic understanding of the geometry and math involved in collision detection. At the end of the article, I’ll provide some references in case you feel a bit rusty in this area. I’ll also assume that you’ve read Jeff Lander’s Graphic Content columns on collision detection (“Crashing into the New Year,” ; “When Two Hearts Collide,”; and “Collision Response: Bouncy, Trouncy, Fun,” ). I’ll take a top-down approach to collision detection by first looking at the whole picture and then quickly inspecting the core routines. I’ll discuss collision detection for two types of graphics engines: portal-based and BSP-based engines. Because the geometry in each engine is organized very differently from the other, the techniques for world-object collision detection are very different. The object-object collision detection, for the most part, will be the same for both types of engines, depending upon your current implementation. After we cover polygonal collision detection, we’ll examine how to extend what we’ve learned to curved objects.

The Big Picture

To create an optimal collision detection routine, we have to start planning and creating its basic framework at the same time that we’re developing a game’s graphics pipeline. Adding collision detection near the end of a project is very difficult. Building a quick collision detection hack near the end of a development cycle will probably ruin the whole game because it’ll be impossible to make it efficient. In a perfect game engine, collision detection should be precise, efficient, and very fast. These requirements mean that collision detection has to be tied closely to the scene geometry management pipeline. Brute force methods won’t work — the amount of data that today’s 3D games handle per frame can be mind-boggling. Gone are the times when you could check each polygon of an object against every other polygon in the scene.

Let’s begin by taking a look at a basic game engine loop (Listing 1). A quick scan of this code reveals our strategy for collision detection. We assume that collision has not occurred and update the object’s position. If we find that a collision has occurred, we move the object back and do not allow it to pass the boundary (or destroy it or take some other preventative measure). However, this assumption is too simplistic because we don’t know if the object’s previous position is still available. You’ll have to devise a scheme for what to do in this case (otherwise, you’ll probably experience a crash or you’ll be stuck). If you’re an avid game player, you’ve probably noticed that in some games, the view starts to shake when you approach a wall and try to go through it. What you’re experiencing is the effect of moving the player back. Shaking is the result of a coarse time gradient (time slice).

Listing 1. Extremely Simplified Game Loop

while(1){
process_input();
update_objects();
render_world();
}

update_objects(){
for (each_object)
save_old_position();
calc new_object_position
{based on velocity accel. etc.}
if (collide_with_other_objects())
new_object_position = old_position();
{or if destroyed object remove it etc.}

}

But our method is flawed. We forgot to include the time in our equation. Figure 1 shows that time is just too important to leave out. Even if an object doesn’t collide at time t1 or t2, it may cross the boundary at time t where t1 < t < t2. This is especially true when we have large jumps between successive frames (such as when the user hit an afterburner or something like that). We’ll have to find a good way to deal with &nbspdiscrepancy as well.

We could treat time as a fourth dimension and do all of our calculations in 4D. These calculations can get very complex, however, so we’ll stay away from them. We could also create a solid out of the space that the original object occupies between time t1 and t2 and then test the resulting solid against the wall (Figure 2).

An easy approach is to create a convex hull around an object’s location at two different times. This approach is very inefficient and will definitely slow down your game. Instead of constructing a convex hull, we could construct a bounding box around the solid. We’ll come back to this problem once we get accustomed to several other techniques.

Another approach, which is easier to implement but less accurate, is to subdivide the given time interval in half and test for intersection at the midpoint. This calculation can be done recursively for each resulting half, too. This approach will be faster than the previous methods, but it’s not guaranteed to catch all of the collisions.

Another hidden problem is the collide_with_other_objects() routine, which checks whether an object intersects any other object in the scene. If we have a lot of objects in the scene, this routine can get very costly. If we have to check each object against all other objects in the scene, we’ll have to make roughly

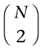
(N choose 2) comparisons. Thus, the number of comparisons that we’ll need to perform is of order N2 (or O(N2)). But we can avoid performing O(N2) pair-wise comparisons in one of several ways. For instance, we can divide our world into objects that are stationary (collidees) and objects that move (colliders) even with a v=0. For example, a rigid wall in a room is a collidee and a tennis ball thrown at the wall is a collider. We can build two spatial trees (one for each group) out of these objects, and then check which objects really have a chance of colliding. We can even restrict our environment further so that some colliders won’t collide with each other — we don’t have to compute collisions between two bullets, for example. This procedure will become more clear as we move on, for now, let’s just say that it’s possible. (Another method for reducing the number of pair-wise comparisons in a scene is to build an octree. This is beyond the scope of this article, but you can read more about octrees in Spatial Data Structures: Quadtree, Octrees and Other Hierarchical Methods, mentioned in the “For Further Info” section at the end of this article.) Now lets take a look at portal-based engines and see why they can be a pain in the neck when it comes to collision detection.

Portal Engines and Object-Object Collisions

Portal-based engines divide a scene or world into smaller convex polyhedral sections. Convex polyhedra are well-suited for the graphics pipeline because they eliminate overdraw. Unfortunately, for the purpose of collision detection, convex polyhedra present us with some difficulties. In some tests that I performed recently, an average convex polyhedral section in our engine had about 400 to 500 polygons. Of course, this number varies with every engine because each engine builds sections using different geometric techniques. Polygon counts will also vary with each level and world.

Determining whether an object’s polygons penetrate the world polygons can be computationally expensive. One of the most primitive ways of doing collision detection is to approximate each object or a part of the object with a sphere, and then check whether spheres intersect each other. This method is widely used even today because it’s computationally inexpensive. We merely check whether the distance between the centers of two spheres is less than the sum of the two radii (which indicates that a collision has occurred). Even better, if we calculate whether the distance squared is less than the sum of the radii squared, then we eliminate that nasty square root in our distance calculation. However, while the calculations are simple, the results are extremely imprecise (Figure 3).

But what if we use this imprecise method as simply a first step. We represent a whole character as one big sphere, and then check whether that sphere intersects with any other object in the scene. If we detect a collision and would like to increase the precision, we can subdivide the big sphere into a set of smaller spheres and check each one for collision (Figure 4). We continue to subdivide and check until we are satisfied with the approximation. This basic idea of hierarchy and subdivision is what we’ll try to perfect to suit our needs.

Using spheres to approximate objects is computationally inexpensive, but because most geometry in games is square, we should try to use rectangular boxes to approximate objects. Developers have long used bounding boxes and this recursive splitting to speed up various ray-tracing routines. In practice, these methods have manifested as octrees and axis-aligned bounding boxes (AABBs). Figure 5 shows an AABB and an object inside it.

“Axis-aligned” refers to the fact that either the box is aligned with the world axes or each face of the box is perpendicular to one coordinate axis. This basic piece of information can cut down the number of operations needed to transform such a box. AABBs are used in many of today’s games; developers often refer to them as the model’s bounding box. Again, the tradeoff for speed is precision. Because AABBs always have to be axis-aligned, we can’t just rotate them when the object rotates — they have to be recomputed for each frame. Still, this computation isn’t difficult and doesn’t slow us down much if we know the extents of each character model. However, we still face precision issues. For example, let’s assume that we’re spinning a thin, rigid rod in 3D, and we’d like to construct an AABB for each frame of the animation. As we can see, the box approximates each frame differently and the precision varies (Figure 6).

So, rather than use AABBs, why can’t we use boxes that are arbitrarily oriented and minimize the empty space, or error, of the box approximation. This technique is based on what are called oriented bounding boxes (OBBs) and has been used for ray tracing and interference detection for quite some time. This technique is not only more accurate, but also more robust than the AABB technique, as we shall see. However, OBBs are lot more difficult to implement, slower, and inappropriate for dynamic or procedural models (an object that morphs, for instance). It’s important to note that when we subdivide an object into more and more pieces, or volumes, we’re actually creating a hierarchical tree of that starting volume.

Our choice between AABBs and OBBs should be based upon the level of accuracy that we need. For a fast-action 3D shooter, we’re probably better off implementing AABB collision detection — we can spare a little accuracy for the ease of implementation and speed. The source code that accompanies this article is available from the Game Developer web site. It should get you started with AABBs, as well as providing some examples of source code from several collision detection packages that also implement OBBs. Now that we have a basic idea of how everything works, let’s look at the details of the implementation.

Building Trees

Creating OBB trees from an arbitrary mesh is probably the most difficult part of the algorithm, and it has to be tweaked and adjusted to suit the engine or game type. Figure 7 shows the creation of successive OBBs from a starting model. As we can see, we have to find the tightest box (or volume, in the case of 3D) around a given model (or set of vertices).

There are several ways to precompute OBBs, and they all involve a lot of math. The basic method is to calculate the mean of the distribution of vertices as the center of the box and then calculate the covariance matrix. We then use two of the three eigenvectors of the covariance matrix to align the box with the geometry. We can also use a convex hull routine to further speed up and optimize tree creation. You can find the complete derivation in the Gottschalk, Lin, and Manocha paper cited in the “For Further Info” section.

Building AABB trees is much easier because we don’t have to find the minimum bounding volume and its axis. We just have to decide where to split the model and we get the box construction for free (because it’s a box parallel with the coordinate axes and it contains all of the vertices from one side of the separating plane).

So, now that we have all of the boxes, we have to construct a tree. We could use a top-down approach whereby we begin with the starting volume and recursively subdivide it. Alternatively, we could use a bottom-up approach, merging smaller volumes to get the largest volume. To subdivide the largest volume into smaller ones, we should follow several suggested rules. We split the volume along the longest axis of the box with a plane (a plane orthogonal to one of its axes) and then partition the polygons based upon which side of the partitioning axis they fall (Figure 7). If we can’t subdivide along the longest axis, we subdivide along the second longest. We continue until we can’t split the volume any more, and we’re left with a triangle or a planar polygon. Depending on how much accuracy we really need (for instance, do we really need to detect when a single triangle is collided?), we can stop subdividing based on some arbitrary rule that we propose (the depth of a tree, the number of triangles in a volume, and so on).

As you can see, the building phase is quite complex and involves a considerable amount of computation. You definitely can’t build your trees during the run time — they must be computed ahead of time. Precomputing trees eliminates the possibility of changing geometry during the run time. Another drawback is that OBBs require a large amount of matrix computations. We have to position them in space, and each subtree has to be multiplied by a matrix.

Detecting Collisions Using Hierarchy Trees

Now, let’s assume that we have either our OBB or AABB trees. How do we actually perform collision detection? We’ll take two trees and check whether two initial boxes overlap. If they do, they might intersect, and we’ll have to recursively process them further (recursive descent). If, along the descent, we find that the subtrees do not intersect, we can stop and conclude that no intersection has occurred. If we find that the subtrees do intersect, we’ll have to process the tree until we hit its leaf nodes to find out which parts overlap. So, the only thing we have to figure out is how to check whether two boxes overlap. One of the tests that we could perform would be to project the boxes on some axis in space and check whether the intervals overlap. If they don’t, the given axis is called a separating axis (Figure 8).

To check quickly for overlap, we’ll use something called the Separating Axis Theorem. This theorem tells us that we have only 15 potential separating axes. If overlap occurs on every single separating axis, the boxes intersect. Thus, it’s very easy to determine whether or not two boxes intersect.

Interestingly, the time gradient problem mentioned earlier could easily be solved by the separating axis technique. Remember that the problem involved determining whether a collision has occurred in between any two given times. If we add velocities to the box projection intervals and they overlap on all 15 axes, then a collision has occurred. We could also use an structure that resembles an AABB tree to separate colliders and collidees and check whether they have a possibility of collision. This calculation can quickly reject the majority of the cases in a scene and will perform in an O(N logN) time that is close to optimal.

Collision Techniques Based on BSP Trees

BSP (Binary Space Partitioning) trees are another type of space subdivision technique that’s been in use for many years in the game industry (Doom was the first commercial game that used BSP trees). Even though BSP trees aren’t as popular today as they have been over the past couple of years, the three most licensed game engines today — Quake II, Unreal, and Lithtech — still use them quite extensively. The beauty and extreme efficiency of BSP trees comes to light when we take a look at collision detection. Not only are BSP trees efficient for geometry culling, we also get very efficient world-object collision almost for free.

The BSP tree traversal is the fundamental technique used with BSPs. Collision detection basically is reduced to this tree traversal, or search. This approach is powerful because it rejects a lot of geometry early, so in the end, we only test the collision detection against a small number of planes. As we’ve seen before, finding a separating plane between two objects is sufficient for determining that those two objects don’t intersect. If a separating plane exists, no collision has occurred. So, we can recursively traverse a world’s tree and check whether separating planes intersect the bounding sphere or bounding box. We can increase the accuracy of this approach by checking for every one of the object’s polygons. The easiest way to perform this check is to test whether all parts of the object are on the same side of the plane. This calculation is extremely simple. We can use the Cartesian plane equation, ax + by + cz + d = 0, to determine the side of the plane upon which the point lies. If the equation is satisfied, then our point lies on the plane. If ax + by + cz + d > 0, then the point is on the positive side the plane. If ax + by + cz + d < 0, then the point is on the negative side the plane.

The only important thing to note is that for a collision not to occur, all of the points of an object (or a bounding box) have to be on either the positive or the negative side of a given plane. If we have points on both the positive and negative side of the plane, a collision has occurred and the plane intersects the given object.

Unfortunately, we have no elegant way of checking whether a collision has occurred in between the two intervals (although the techniques discussed at the beginning of this article still apply). However, I have yet to see another structure that has as many uses as a BSP tree.

Curved Objects and Collision Detection

Now that we’ve seen two approaches to collision detection for polygonal objects, lets see how we can compute the collision of curved objects. Several games will be coming out in 1999 that use curved surfaces quite extensively, so the efficient collision detection of curved surfaces will be very important in the coming year. The collision detection (which involves exact surface evaluation at a given point) of curved surfaces is extremely computationally intensive, so we’ll try to avoid it. We’ve already discussed several methods that we could use in this case, as well. The most obvious approach is to approximate the curved surface with a lowest-tessellation representation and use this polytope for collision detection. An even easier, but less accurate, method is to construct a convex hull out of the control vertices of the curved surface and use it for the collision detection. In any case, curved surface collision approximation is very similar to general polytope collision detection. Figure 9 shows the curved surface and the convex hull formed from the control vertices.

If we combined both techniques into a sort of hybrid approach, we could first test the collision against the hull and then recursively subdivide the patch to which the hull belongs, thus increasing the accuracy tremendously.

Decide for Yourself

Now that we’ve gone over some of the more advanced collision detection schemes (and some basic ones, too), you should be able to decide what type of system would best suit your own game. The main thing you’ll have to decide is how much accuracy you’re willing to sacrifice for speed, simplicity of implementation (shorter development time), and flexibility.

For Further Info

• H. Samet. Spatial Data Structures: Quadtree, Octrees and Other Hierarchical Methods. Addison Wesley, 1989.

• For more information about AABBs take a look at J. Arvo and D. Kirk. “A survey of ray tracing acceleration techniques,” An Introduction to Ray Tracing. Academic Press, 1989.

• For a transformation speedup, check out James Arvo’s paper in Andrew S. Glassner, ed. Graphics Gems. Academic Press, 1990.

• S. Gottschalk, M. Lin, and D. Manocha. “OBBTree: A hierarchical Structure for rapid interference detection,” Proc. Siggraph 96. ACM Press, 1996. has contributed a great deal to the discussion of OBBs in terms of accuracy and speed of execution.

• S. Gottschalk. Separating Axis Theorem, TR96-024, UNC Chapel Hill, 1990.

• N. Greene. “Detecting intersection of a rectangular solid and a convex polyhedron,” Graphics Gems IV. Academic Press, 1994. introduces several techniques that speed up the overlap computation of a box and a convex polyhedron.

Nick Bobic is trying not to work 14 hours a day with very little success. Any new collision tips and tricks should be sent to [email protected].