Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.
Performance is key in games -- here, experienced games programmer Gustavo Oliveira delivers a comparison of libraries that should increase your performance and cut down on code bloat, and contrasts different compilers.

Inside most 3D applications there exists a vector library to perform routine calculations such as vector arithmetic, logic, comparison, dot and cross products, and so on. Although there are countless ways to go about designing this type of library, developers often miss key factors to allow a vector library to perform these calculations the fastest possible way.
Around late 2004 I was assigned to develop such a vector library code-named VMath, standing for "Vector Math." The primary goal of VMath was not only to be the fastest but also easily portable across different platforms.
To my surprise in 2009, the compiler technology has not changed much. Indeed the results presented in this article resulted from my research during that time, with some exceptions, are nearly the same that when I was working on VMath five years ago.
Since this article is mostly written in C++ and focused primarily in performance, defining the fastest library can be misleading sometimes.
Therefore, the fastest library as described in here, is the one that generates the smallest assembly code compared to other libraries when compiling the same code using the same settings (assuming release mode of course). This is because the fastest library generates fewer instructions to perform the same exact calculations. Or in other words, the fastest library is the one the bloats the code the least.
With the wide spread of single instruction multiple data instructions (SIMD) around modern processors the task of developing a vector library has become much easier. SIMD operations work on SIMD registers precisely as FPU operations on FPU registers. However, the advantage is that SIMD registers are usually 128-bit wide forming the quad-word: four "floats" or "ints" of 32-bits each. This allows developers to perform 4D vector calculations with a single instruction. Because of that, the best feature a vector library can have is to take advantage of the SIMD instructions in it.
Nonetheless, when working with SIMD instructions you must watch out for common mistakes that can cause the library to bloat the code. In fact the code bloat of a SIMD vector library can be drastic to a point that it would have been better to simply use FPU instructions.
The best way to talk to SIMD instructions when designing a high level interface of a vector library is by the usage of intrinsics. They are available from most compilers that target processors with SIMD instructions. Also, each instrisics translates into a single SIMD instruction. However the advantage of using intrinsics instead of writing assembly directly is to allow the compiler to perform scheduling and expression optimization. That can significantly minimize code bloat.
Examples of instrinsics below:
Intel & AMD:
vr = _mm_add_ps(va, vb);
Cell Processor (SPU):
vr = spu_add(va, vb);
Altivec:
vr = vec_add(va, vb);
By observing the intrisics interface a vector library must imitate that interface to maximize performance. Therefore, you must return the results by value and not by reference, as such:
//correct
inline Vec4 VAdd(Vec4 va, Vec4 vb)
{
return(_mm_add_ps(va, vb));
};
On the other hand if the data is returned by reference the interface will generate code bloat. The incorrect version below:
//incorrect (code bloat!)
inline void VAddSlow(Vec4& vr, Vec4 va, Vec4 vb)
{
vr = _mm_add_ps(va, vb);
};
The reason you must return data by value is because the quad-word (128-bit) fits nicely inside one SIMD register. And one of the key factors of a vector library is to keep the data inside these registers as much as possible. By doing that, you avoid unnecessary loads and stores operations from SIMD registers to memory or FPU registers. When combining multiple vector operations the "returned by value" interface allows the compiler to optimize these loads and stores easily by minimizing SIMD to FPU or memory transfers.
Here, "pure data" is defined as data declared outside a "class" or "struct" by a simple "typedef" or "define". When I was researching various vector libraries before coding VMath, I observed one common pattern among all libraries I looked at during that time. In all cases, developers wrapped the basic quad-word type inside a "class" or "struct" instead of declaring it purely, as follows:
class Vec4
{
...
private:
__m128 xyzw;
};
This type of data encapsulation is a common practice among C++ developers to make the architecture of the software robust. The data is protected and can be accessed only by the class interface functions. Nonetheless, this design causes code bloat by many different compilers in different platforms, especially if some sort of GCC port is being used.
An approach that is much friendlier to the compiler is to declare the vector data "purely", as follows:
typedef __m128 Vec4;
Admittedly a vector library designed that way will lose the nice encapsulation and protection of its fundamental data. However the payoff is certainly noticeable. Let's look at an example to clarify the problem.
We can approximate the sine function by using Maclaurin (*) series as below:
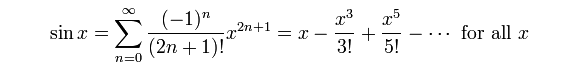
(*) There are better and faster ways to approximate the sine function in production code. The Maclaurin series is used here just for illustrative purposes.
If a developer codes a vector version of a sine function using the formula above the code would look like more or less:
Vec4 VSin(const Vec4& x)
{
Vec4 c1 = VReplicate(-1.f/6.f);
Vec4 c2 = VReplicate(1.f/120.f);
Vec4 c3 = VReplicate(-1.f/5040.f);
Vec4 c4 = VReplicate(1.f/362880);
Vec4 c5 = VReplicate(-1.f/39916800);
Vec4 c6 = VReplicate(1.f/6227020800);
Vec4 c7 = VReplicate(-1.f/1307674368000);
Vec4 res = x +
c1*x*x*x +
c2*x*x*x*x*x +
c3*x*x*x*x*x*x*x +
c4*x*x*x*x*x*x*x*x*x +
c5*x*x*x*x*x*x*x*x*x*x*x +
c6*x*x*x*x*x*x*x*x*x*x*x*x*x +
c7*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x;
return (res);
}
Now let's look at the assembler of the same function compiled as Vec4 declared "purely" (left column) and declared inside a class (right column). (Click here to download the table document. Refer to Table 1.)
The same exact code shrinks by a factor of approximate 15 percent simply by changing how the fundamental data was declared. If this function was performing some inner loop calculation, there would not only be savings in code size but certainly would run faster.
Another nice C++ feature that became popular in most modern applications due to its clarity is the use of overloaded operators. However, as a general rule, overloaded operators bloat the code as well. A fast SIMD vector library should also provide a procedural C-like interface.
The code bloat generated from overloaded operators does not arise when dealing with simple math expressions. This is probably why most developers ignore this problem when first designing a vector library. However, as the expressions get more complex the optimizer has to do extra work to assure correct results. This involves creating unnecessary temporary storage variables that usually translate into more load/store operations between SIMD registers and memory.
Let's try to compile a 3-band equalizer filter using overloaded operators and a procedural interface as an example. Then we look at the generated assembly code. The source code written with overloaded operators looks like:
Vec4 do_3band(EQSTATE* es, Vec4& sample)
{
Vec4 l,m,h;
es->f1p0 += (es->lf * (sample - es->f1p0)) + vsa;
es->f1p1 += (es->lf * (es->f1p0 - es->f1p1));
es->f1p2 += (es->lf * (es->f1p1 - es->f1p2));
es->f1p3 += (es->lf * (es->f1p2 - es->f1p3));
l = es->f1p3;
es->f2p0 += (es->hf * (sample - es->f2p0)) + vsa;
es->f2p1 += (es->hf * (es->f2p0 - es->f2p1));
es->f2p2 += (es->hf * (es->f2p1 - es->f2p2));
es->f2p3 += (es->hf * (es->f2p2 - es->f2p3));
h = es->sdm3 - es->f2p3;
m = es->sdm3 - (h + l);
l *= es->lg;
m *= es->mg;
h *= es->hg;
es->sdm3 = es->sdm2;
es->sdm2 = es->sdm1;
es->sdm1 = sample;
return(l + m + h);
}
Now the same code re-written using a procedural interface:
Vec4 do_3band(EQSTATE* es, Vec4& sample)
{ Vec4 l,m,h;
es->f1p0 = VAdd(es->f1p0, VAdd(VMul(es->lf, VSub(sample, es->f1p0)), vsa));
es->f1p1 = VAdd(es->f1p1, VMul(es->lf, VSub(es->f1p0, es->f1p1)));
es->f1p2 = VAdd(es->f1p2, VMul(es->lf, VSub(es->f1p1, es->f1p2)));
es->f1p3 = VAdd(es->f1p3, VMul(es->lf, VSub(es->f1p2, es->f1p3)));
l = es->f1p3;
es->f2p0 = VAdd(es->f2p0, VAdd(VMul(es->hf, VSub(sample, es->f2p0)), vsa));
es->f2p1 = VAdd(es->f2p1, VMul(es->hf, VSub(es->f2p0, es->f2p1)));
es->f2p2 = VAdd(es->f2p2, VMul(es->hf, VSub(es->f2p1, es->f2p2)));
es->f2p3 = VAdd(es->f2p3, VMul(es->hf, VSub(es->f2p2, es->f2p3)));
h = VSub(es->sdm3, es->f2p3);
m = VSub(es->sdm3, VAdd(h, l));
l = VMul(l, es->lg);
m = VMul(m, es->mg);
h = VMul(h, es->hg);
es->sdm3 = es->sdm2;
es->sdm2 = es->sdm1;
es->sdm1 = sample;
return(VAdd(l, VAdd(m, h)));
}
Finally let's look at the assembly code of both (click here to download the table document; refer to Table 2.)
The code that used procedural calls was approximately 21 percent smaller. Also notice that this code is equalizing four streams of audio simultaneously. So, compared to doing the same calculation on the FPU the speed boost would be tremendous.
I shall emphasize that I do not discourage the support for overloaded operators on a vector library. Indeed I encourage providing both so that developers can write procedurally if the expressions get complex enough to create code bloat.
In fact when I was testing VMath, I often wrote first my math expressions using overloaded operators. Then I tested the same code using procedural calls to see if any difference appeared. The code bloat was dependent upon the complexity of the expressions as stated before.
The inline key word allows the compiler to get the rid of expensive function calls and therefore optimizing the code at the price of more code bloat. It's a common practice to inline all vector functions so that function calls are not performed.
Windows compilers (Microsoft & Intel) are really impressive about when to or not to inline functions. It's best to leave this job to the compiler, so there is nothing to lose by adding inline to all your vector functions.
However one problem with inline is that the instruction cache misses (I-Cache). If the compiler is not good enough to realize when a function is "too big" for the target platform, you can fall on a big problem. The code will not only bloat but also make lots of I-Cache misses. Then vector functions can go much slower.
I could not come up with one case in Windows development that had an "inlined" vector function which caused code bloat to a point that the I-Cache was affected. In fact, even when I don't inline functions the windows compilers are smart enough to inline them for me. However, when I did PSP and PS3 development the GCC port was not so smart. Indeed there had been cases that was better not to inline.
But if you fall into these specific cases, it's always trivial to wrap your inline function to a platform-specific call that is not "inlined" such as:
Vec4 DotPlatformSpecific(Vec4 va, Vec4 vb)
{
return (Dot(va, vb));
}
On the other hand, if the vector library is designed without inline you cannot force them to inline easily. So you rely on the compiler to be smart enough to inline the functions for you. Which may not work as you expect on different platforms.
When working with SIMD instructions doing one calculation and four takes the same time. But what if you don't need the result of the four registers? It's still to your advantage to replicate the result into the SIMD register, if the implementation is the same. By replicating results into the SIMD quad-word, it can help the compiler optimize vector expressions.
For similar reasons it's important to provide data accessors such as GetX, GetY, GetZ, and GetZ. By providing this type of interface, and assuming the developer uses it, the vector library can minimize expensive casting operations between SIMD registers and FPU registers.
Shortly I will discuss a classic example that illustrates this problem.
Even if a well-designed vector library is available, and especially when working with SIMD instructions, you must to pay attention on how you use it. Relying completely on the compiler to generate the best code is not a good idea.
Depending how write you code it can affect significantly the final assembled code. Even by using robust compilers the difference will not go unnoticed. Back to the Sine example, if that function was written by using smaller expressions the final code would have been much more efficient. Let's look at a new version of the same code as follows:
Vec4 VSin2(const Vec4& x)
{
Vec4 c1 = VReplicate(-1.f/6.f);
Vec4 c2 = VReplicate(1.f/120.f);
Vec4 c3 = VReplicate(-1.f/5040.f);
Vec4 c4 = VReplicate(1.f/362880);
Vec4 c5 = VReplicate(-1.f/39916800);
Vec4 c6 = VReplicate(1.f/6227020800);
Vec4 c7 = VReplicate(-1.f/1307674368000);
Vec4 tmp0 = x;
Vec4 x3 = x*x*x;
Vec4 tmp1 = c1*x3;
Vec4 res = tmp0 + tmp1;
Vec4 x5 = x3*x*x;
tmp0 = c2*x5;
res = res + tmp0;
Vec4 x7 = x5*x*x;
tmp0 = c3*x7;
res = res + tmp0;
Vec4 x9 = x7*x*x;
tmp0 = c4*x9;
res = res + tmp0;
Vec4 x11 = x9*x*x;
tmp0 = c5*x11;
res = res + tmp0;
Vec4 x13 = x11*x*x;
tmp0 = c6*x13;
res = res + tmp0;
Vec4 x15 = x13*x*x;
tmp0 = c7*x15;
res = res + tmp0;
return (res);
}
Now let's compare the results. (Click here to download the table data. Refer to Table 3.)
The code shrunk by almost 40% by simply re-writing in a more friendly way to the compiler.
As stated before, casting operation between SIMD registers and FPU registers can be expensive. A classic example of when this happens is the "dot product" which results one scalar from two vectors, as such:
Dot (Va, Vb) = (Va.x * Vb.x) + (Va.y * Vb.y) + (Va.z * Vb.z) + (Va.w * Vb.w);
Now let's take a look at this code snipped that uses a dot product:
Vec4& x2 = m_x[i2];
Vec4 delta = x2-x1;
float deltalength = Sqrt(Dot(delta,delta));
float diff = (deltalength-restlength)/deltalength;
x1 += delta*half*diff;
x2 -= delta*half*diff;
By inspecting the code above, "deltalength" is the distance between vector "x1" and vector "x2". So the result of the "Dot" function is scalar. Then this scalar is used and modified throughout the rest of the code to scale vector "x1" and "x2". Clearly there are lots of casting operations going on from vector to scalar and vice-versa. This is expensive since the compiler needs to generate code that will move data from and to the SIMD and FPU registers.
However, if we assume the "Dot" function above replicates the result into the SIMD 4-quad words and the "w" component zeroed-out, there is really no difference in re-writing the code as follows:
Vec4& x2 = m_x[i2];
Vec4 delta = x2-x1;
Vec4 deltalength = Sqrt(Dot(delta,delta));
Vec4 diff = (deltalength-restlength)/deltalength;
x1 += delta*half*diff;
x2 -= delta*half*diff;
Because "deltalength" now has the same result replicated into the quad-word, the expensive casting operations are no longer necessary.
Whenever possible, by re-arranging your data you can take advantage of a vector library. For example, when working with audio you can store your data stream to be SIMD friendly.
Let's say you have four streams of audio samples stored in four different arrays as such:
Bass audio samples array:
B0 | B1 | B2 | B3 | B4 | B5 | B6 | B7 | Etc... |
Drums audio samples array:
D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | Etc... |
Guitar audio samples array:
G0 | G1 | G2 | G3 | G4 | G5 | G6 | G7 | Etc... |
Trumpet audio samples array:
T0 | T1 | T2 | T3 | T4 | T5 | T6 | T7 | Etc... |
But you can also interleave these audio channels and store the same data as:
Full band audio samples array:
B0 | D0 | G0 | T0 | B1 | D1 | G1 | T1 | Etc... |
The advantage is that now you can load your array directly into the SIMD registers and perform calculations on all samples simultaneously. The disadvantage is that if you need to pass that data to another system that requires four streamlined arrays, you will have re-organize that data back to its original form. Which can be expensive and memory intense if the vector library is not performing heavy calculations on the data.
Microsoft ships DirectX with XNA Math that runs on Windows and Xbox 360. XNA Math is a vector library that has a FPU vector interface (for backwards compatibility) and a SIMD interface.
Although back in late 2004 I did not have access to XNA Math Library (if it existed that time), I was happy to discover now that XNA Math uses the precisely the same interface I had used in VMath five years ago. The only difference was the target platform, which was in my case was Windows, PS3, PSP, and PS2.
XNA Math is designed using the key features of a SIMD vector library described in here. It returns results by values, the vector data is declared purely, it has a support for overloaded operators and procedural calls, inline all vector functions, provide data accessors, and so on.
When two independent developers come up with the same results, it's highly likely you are close to the "as fast as it can be". So if you are faced with the task of coding a vector library your best bet for a cross-platform SIMD vector library is to follow the steps of XNA Math or VMath.
With that in mind, you may ask, can XNA Math be faster? As far as interfacing with the SIMD instructions, I don't believe so. However, the beauty of having the fastest interface is that what's left is purely the implementation of the functions.
If one can come up with a faster version of a function with the same interface, it is just a matter of plugging in the new code and you are done. But if you are working on a vector library that does not provide a good interface with the SIMD instructions, coming up with a better implementation may still leave you behind.
Assuming you are working on high-level code, being faster than XNA Math is quite difficult. The options left are: optimize its functions or find flaws on a well-revised library, if they exist. But also as stated earlier, even if you are working with XNA Math and you don't know how to use it to its full potential you can bloat the code and be left behind.
To attempt such a challenge I searched for algorithms that could make the difference be noticeable when compiled by VMath or XNA Math. I knew that algorithms involving only trivial calculations would run at the same speed. Therefore, the algorithms had to have some sort of mathematical complexity involved.
With that in mind, my final choices were to port a DSP code that performs a 3-band equalizer on audio data and a cloth simulator. The URLs to original sample codes can be found at the references, along with their respective authors.
I tried as much as I could to keep the original author's code intact so that it feels like a port and not a different implementation. The 3-band equalizer code was straightforward, but I had to add few extra lines specifically for the cloth simulation.
During the implementation, I also included into the sample code a generic vector class, here called VClass, that does not follow the key features of VMath or XNA Math. It's a standard vector class where the data is encapsulated inside a class and does not provide a procedural interface. I also ported the code to VClass just for performance comparison.
For the equalizer algorithm I admittedly cheated. There was not much I could do to my implementation of VMath compared to XNA Math. Precisely what I did was to port the equalizer code using XNA Math and overloaded operators. Then for VMath I did the same but using procedural calls, because I knew overloaded operators would bloat the code.
However, my cheat had a purpose, and it was again to demonstrate that even if you are working on the fastest vector library, you could fall behind if unaware of how compilers are generating the code.
Also I prepared the data to be SIMD friendly. So the audio channels are interleaved so that the loads and stores are minimized. However, to play the channels I had to re-organize the data to be sent to XAudio2 as four arrays of streamlined PCM audio data. That caused lots of loads and stores. For that reason I also included an FPU version that performs the calculations directly to another copy of the data that is stored as plain arrays of audio samples. The only advantage of the FPU version was no re-organization of data arrays.
Click here for the assembly code generated by VMath and XNA Math -- refer to Table 4.
The results are very similar to what I have shown during the discussion of "Overloaded Operators vs. Procedural Interface" (Table 2). The figure below shows a screenshot of the demo with runtime statistics.
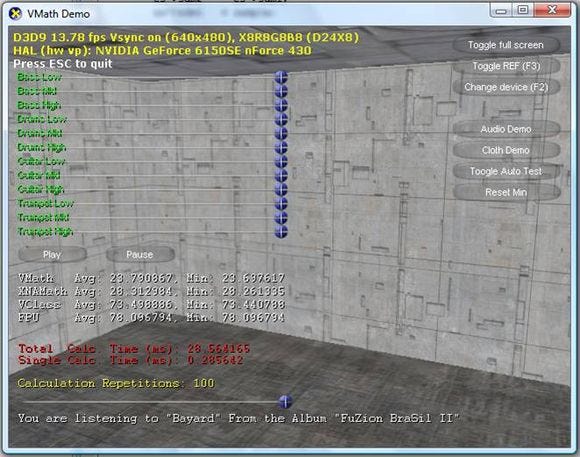
Figure. 1 - Three Band Equalizer
The final statistics are also re-written on the table below for clarity.
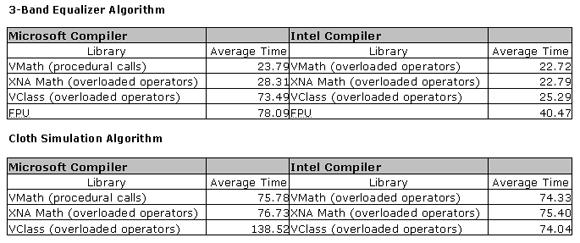
Library | Average Time |
|---|---|
VMath (procedural calls) | 23.79 |
XNA Math (overloaded operators) | 28.31 |
VClass | 73.49 |
FPU (*) | 78.09 |
Using VMath as reference, it was able to go approximately 16 percent faster on average than XNA Math by simply using a different interface call. Even with massive loads and stores to re-compose the audio data to be passed to XAudio2; it was able to go more than three times faster than the FPU version. Which is indeed quite impressive.
Notice also that the VClass was just only 5 percent faster than the FPU version due to the huge amount of code bloat created under the hood.
The simulation algorithm has two main loops where most of the calculations occur. One is the "Verlet" integrator shown below:
void Cloth::Verlet()
{
XMVECTOR d1 = XMVectorReplicate(0.99903f);
XMVECTOR d2 = XMVectorReplicate(0.99899f);
for(int i=0; i
{
XMVECTOR& x = m_x[i];
XMVECTOR temp = x;
XMVECTOR& oldx = m_oldx[i];
XMVECTOR& a = m_a[i];
x += (d1*x)-(d2*oldx)+a*fTimeStep*fTimeStep;
oldx = temp;
}
}
The second is the constraint solver that uses Gauss-Seidel iteration loop to find the solution for all constraints shown below:
void Cloth::SatisfyConstraints()
{
XMVECTOR half = XMVectorReplicate(0.5f);
for(int j=0; j
{
m_x[0] = hook[0];
m_x[cClothWidth-1] = hook[1];
for(int i=0; i
{
XMVECTOR& x1 = m_x[i];
for(int cc=0; cc
{
int i2 = cnstr[i].cIndex[cc];
XMVECTOR& x2 = m_x[i2];
XMVECTOR delta = x2-x1;
XMVECTOR deltalength = XMVectorSqrt(XMVector4Dot(delta,delta));
XMVECTOR diff = (deltalength-restlength)/deltalength;
x1 += delta*half*diff;
x2 -= delta*half*diff;
}
}
}
}
By inspecting the code, changing overloaded operators to procedural calls won't do much. The mathematical expressions are simple enough that the optimizer should generate the same code.
I also removed the floating casting from the original code as described in "Keep Results Into SIMD Registers." Now the loop is pretty tight and SIMD friendly, so what's left? The only thing left is to look inside XNA Math to see if there is anything else that can be done.
It turned out that there was. First by looking at the XMVector4Dot, it is implemented as:
XMFINLINE XMVECTOR XMVector4Dot(FXMVECTOR V1, FXMVECTOR V2)
{ XMVECTOR vTemp2 = V2;
XMVECTOR vTemp = _mm_mul_ps(V1,vTemp2);
vTemp2 = _mm_shuffle_ps(vTemp2,vTemp,_MM_SHUFFLE(1,0,0,0));
vTemp2 = _mm_add_ps(vTemp2,vTemp);
vTemp = _mm_shuffle_ps(vTemp,vTemp2,_MM_SHUFFLE(0,3,0,0));
vTemp = _mm_add_ps(vTemp,vTemp2);
return _mm_shuffle_ps(vTemp,vTemp,_MM_SHUFFLE(2,2,2,2));
}
The implementation is composed by 1 multiplication, 3 shuffles, and 2 adds.
So, I went and wrote a different SSE2 4D Dot that produces the same results but with one less shuffle instruction, as follows:
inline Vec4 Dot(Vec4 va, Vec4 vb)
{
Vec4 t0 = _mm_mul_ps(va, vb);
Vec4 t1 = _mm_shuffle_ps(t0, t0, _MM_SHUFFLE(1,0,3,2));
Vec4 t2 = _mm_add_ps(t0, t1);
Vec4 t3 = _mm_shuffle_ps(t2, t2, _MM_SHUFFLE(2,3,0,1));
Vec4 dot = _mm_add_ps(t3, t2);
return (dot);
}
Unfortunately, to my surprise, my new 4D Dot did not make much of a difference, likely because it had more interdependencies between instructions.
As I looked further, I found one puzzling detail on XNA Math. It calls the reciprocal function to perform its divide. In fact the function chained by multiple calls from the overloaded operator as such:
XMFINLINE XMVECTOR XMVectorReciprocal(FXMVECTOR V)
{
return _mm_div_ps(g_XMOne,V);
}
XMFINLINE XMVECTOR operator/ (FXMVECTOR V1,FXMVECTOR V2)
{
XMVECTOR InvV = XMVectorReciprocal(V2);
return XMVectorMultiply(V1, InvV);
}
The only problem is that it loads the "g_XMOne" and then calls the intrinsics to perform the divide. I am not quite clear why Microsoft implemented this way, but it would have been better to simply call the divide directly. So for VMath I implemented this way, meaning without extra loads as such:
inline Vec4 VDiv(Vec4 va, Vec4 vb)
{
return(_mm_div_ps(va, vb));
};
Now let's look at the assembler of the "Verlet" and "Constraint Solver" using both libraries, with the small optimizations implemented in VMath.
Click here to download the Table document -- refer to Table 5 and Table 6.
Although, I wrote the "Verlet" function using procedural calls for VMath and overloaded operators for XNA Math, there was no difference. I expect the math expressions were not complex enough to cause code bloat. However, the "Contraint Solver" got precisely one instruction smaller due to the faster divide. I highlighted the extra load of the "g_XMOne" on the table that likely the cause of the extra movaps instruction. The screen shot below shows the results.
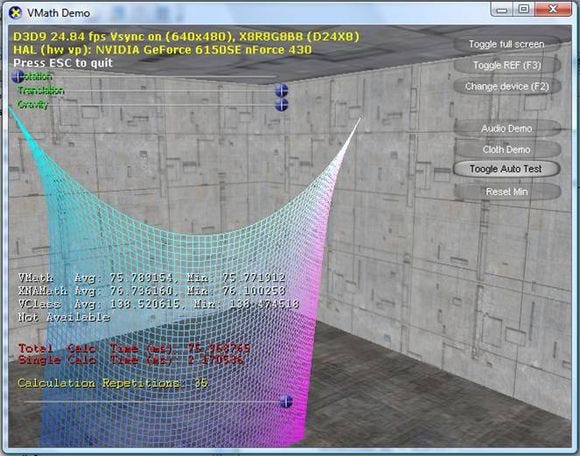
Figure. 2 - Cloth Simulation
Library | Average Time |
|---|---|
VMath (procedural calls) | 75.78 |
XNA Math (overloaded operators) | 76.73 |
VClass | 138.52 |
FPU | Not Implemented |
Technically it was a knockout by VMath because of one instruction; however, the statistics were not sufficient enough to show significant speed boost -- approximately only 1 percent faster.
In fact the results were so close that they floated depending on other factors, such as the OS doing some background tasks. Because of this kind of result, the conclusion is that VMath and XNA Math were practically even.
Nonetheless, both libraries were able to go approximately 50 percent faster than VClass. This is still impressive, counting the fact that the major difference is how the libraries interface with the same intrinsics.
The Microsoft compiler that ships with Visual Studio so far performed all the tests. Now it's time to switch gears and compile the same code with the Intel Compiler.
I have heard about the Intel Compiler before and its reputation of being the fastest. When I built the sample code with Intel, I was really impressed. Indeed Intel has produced a phenomenal compiler that gave me not only faster results, generally speaking, but also unexpected ones.
Let's start by checking out the assembler dump of the three-band equalizer compared to the code compiled using the Microsoft compiler.
Click here to download the table document -- please refer to Table 7.
The Intel compiler was able to shrink the code by about 20 percent. And the result for the "Verlet Integrator" and the "Constraint Solver" respectively were about 7 percent and 6 percent smaller.
But what was the real "Black Magic" was that the generic VClass made the code get even smaller. As I inspected the code the Intel compiler does better with overloaded operators than procedural calls. Another interesting result is that the data encapsulation inside a class bloats the code very little, and in fact for the cloth did not at all. This made all the demo statistics flatten more or less.
Here are the screenshots of the cloth demo using the Intel Compiler.
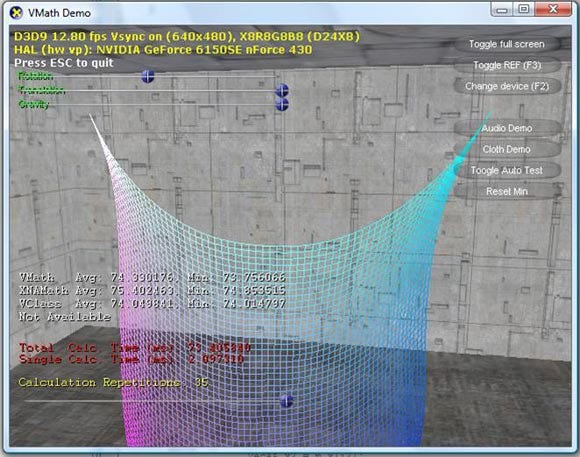
Figure 3 - Cloth Demo Using Intel Compiler
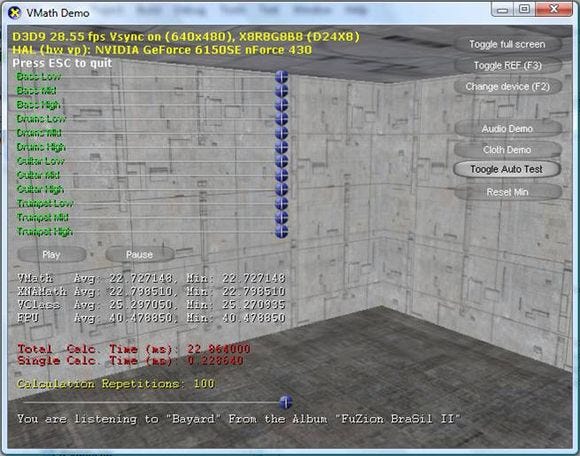
Figure 4 - Three Band EQ Using Intel Compiler
Now all the statistics together for comparison:
Although the Intel compiler has solved the problem of code bloat generated by data inside a class and overloaded operators, I still do not endorse this approach for a cross platform SIMD library. This is because I have done similar tests with six different compilers GCC and SN systems for PS2, PSP, and PS3 -- and they all produce worse results than the Microsoft compiler, meaning they bloat the code even more. So, unless you are specifically writing a library that will only run on Windows, your best bet is to still follow the key points of this article for your SIMD vector library.
The sample code of this article along with all the comparison tables can be downloaded from the URL below:
http://www.guitarv.com/ComputerScience.aspx?page=articles
References:
[1] Microsoft, XNA Math Library Reference
[2] Intel, SHUFPS -- Shuffle Single-Precision Floating-Point Values
[3] Jakobsen, Thomas, Advanced Character Physics
[4] C., Neil, 3 Band Equaliser
[5] Wikipedia, Taylor Series
Read more about:
FeaturesYou May Also Like