Hardware Accelerated Spherical Environment Mapping Using Texture Matrices

Because of the problems with creating the texture maps and the computational costs during runtime, real-time spherical environment mapping is not often used in games. As a result, when the technique is used, the spherical maps are usually pre-calculated and therefore the don't reflect changes in a scene as they happen. Fortunately, some DirectX 7-capable video cards support cubic environment maps, which don't exhibit any of the problems associated with spherical maps, and thus they're suitable for reflecting dynamic scenes. Despite their limitations though, spherical environment maps are still useful. Using sphere maps, you can create very high performance and cheap static reflections which in most cases are good enough for game reflections, another very useful example is creating realistic specular highlights from an infinite light source.

This article will show a hardware T&L accelerated method of using sphere maps, it is assumed that your game will have some level of geometry hardware acceleration in addition to Direct3D support. If geometry acceleration is not present, applying these techniques may actually slow down a game (especially if the standard Direct3D software pipeline is used).

The Spheremap Demo

To begin our look at spherical mapping let's look at the Spheremap demo, one of the samples that comes with DirectX 7 (to find this demo, search the DirectX 7 CD-ROM for SPHEREMAP.EXE). This application displays a spherically environment-mapped teapot. Figure 1 shows a screenshot from this application.

The Spheremap demo implements what I call "normal" spherical mapping, where the normal vector at a vertex is used in place of the eye-to-vertex reflection vector. The code that performs the mapping within this demo is shown in listing 1 (in the DirectX SDK source file this can be found in a function named ApplySphereMapToObject() ).

Unfortunately, the Spheremap demo has many shortcomings and doesn't implement spherical reflection mapping like OpenGL (when the automatic texture address generation is set to GL_SPHERE_MAP). In fact, Direct3D has no sphere map support at all - you have to calculate the texture coordinates yourself. To do so, you could create a system that cycled through all of the vertices and have the CPU calculate the texture coordinates, this is what the DirectX7 Spheremap demo does but this is far from efficient.

A closer look

The DirectX 7 documentation and various pieces of literature from the graphics vendors stress over and over that correctly using and managing vertex buffers is the key to getting high performance - especially with hardware T&L-based cards. Static vertex buffers are the most efficient, as they can be kept in local video memory and never updated (i.e. optimized), but that means that all geometry processing has to be performed with the standard hardware pipeline, limiting the effects that you can create. Even so, it is surprising what can be done when all the resources of the pipeline are used.

If you must have dynamic geometry, a carefully managed CPU-modifiable vertex buffer is still better than no vertex buffer (as in the the SPHEREMAP.EXE example). However, the Spheremap sample code is one of those pathological cases where vertex buffers are actually slower - if you converted that code to use video memory vertex buffers, it would most certainly slow down since the normal is read back from the vertex buffer (which is taboo, as both video memory and AGP memory are uncached). If the vertex buffer happens to be in local video memory, then it's being fetched back over the AGP bus, which is painfully slow. In this case, keeping a second copy of the normal vectors in system memory would be best.

Also, note that there's a glaring mistake in the DirectX algorithm, which I am compelled to point out. It is the line commented, "Check the z-component, to skip any vertices that face backwards". Vertices do not face backwards, polygons do; it is perfectly legal for a polygon to have a vertex normal that points away from the viewer while still having a face normal pointing towards the viewer:

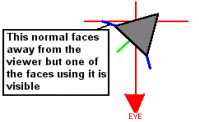
The results of the erroneous z-component check can be seen in the DirectX 7 example when the bottom of the teapot comes into view. For a few frames, a number of triangles are not textured properly. This check is not only an error, it causes the loop to run slower (well, it certainly doesn't speed it up). Without the check, there would be 2N dot products (where N is the number of vertices). With the check in place, and assuming half of the vertices face away from the viewer, there are N+2N/2 = N+N = 2N vertices, so the same amount of work is done. The difference is that now there is a jump in the middle of the loop in which the CPU has to predict or mispredict. On a Pentium II or III, a mispredicted jump is far more expensive than a couple of dot products.

A Closer Look: Vertex Buffers

When you have removed the z-component check, all that's left to do in the main loop is generate texture coordinates. The vector [m11, m21, m31] is the local space +X direction in camera space and the vector [m12, m22, m32] is local space +Y direction in camera space. Recall that all normal vectors are points on a unit sphere, so the code generating the texture coordinates is effectively calculating the longitude and latitude coordinates of the normal vectors position on that sphere (or the cosines of them) by taking the dot product of the unit normal with the unit axes (see Figure 2a & 2b). The output of that calculation is scaled and biased so that the center of the sphere map is the origin:

If we consider that the sphere map UV coordinate calculation requires two dot products, and a matrix*vector performs four dot products we should be able to perform the same calculation using a texture matrix. Direct3D supports 4x4 texture matrices at every texture stage so all we have to make a texture matrix that performs the same dot products as discussed above, also by carefully creating the texture matrix the scale and bias is automatically performed so the origin is in the center of the texture map. The required texture matrix looks like the following:

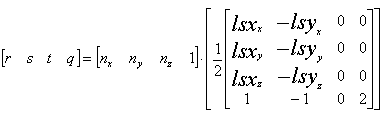
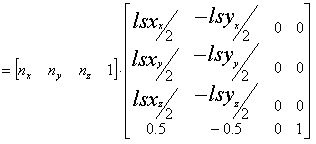
NOTE: In the above math, the vectors lsx and lsy are used in place of [m11, m21, m31] and [m12, m22, m32] to represent the local space x and y axis in camera space - in other words, the local space [1,0,0] and [0,1,0] vectors respectively, transformed by the local*world matrices.

Next, specify the vertex normal as the first three elements of the input texture coordinate vector, and the forth element will automatically be set to its default of 1. The specified texture matrix will be applied to the texture coordinates (normal vector) and the resulting texture coordinated vector identical to that in the DirectX example.

Note: DirectX has no specific naming convention for the elements of a 4D texture coordinate so I will use the standard of [r, s, t, q]. While performing standard 2D texture mapping 'r' component is equivalent to 'u', likewise the 's' component is 'v' and elements 't' and 'q' are unused.

The following code sets the above texture matrix at stage 0. This operation needs to be done any time either the world or local matrices change, as LocalToEyeMat = Local*World:

D3DMATRIX tex = IdentityMatrix;
tex_mat._11 = 0.5f*LocalToEyeMat._11;
tex_mat._21 = 0.5f*LocalToEyeMat._21;
tex_mat._31 = 0.5f*LocalToEyeMat._31;
tex_mat._41 = 0.5f;
tex_mat._12 = -0.5f*LocalToEyeMat._12;
tex_mat._22 = -0.5f*LocalToEyeMat._22;
tex_mat._32 = -0.5f*LocalToEyeMat._32;
tex_mat._42 = -0.5f;

3DDevice->SetTransform(D3DTRANSFORMSTATE_TEXTURE0, &tex_mat);

There is one additional render state that needs to be set. You must tell Direct3D to apply the texture matrix and to use just the first two elements of the result:

3DDevice->SetTextureStageStat ( 0, D3DTSS_TEXTURETRANSFORMFLAGS, D3DTTFF_COUNT2 );

Direct3D has no way of specifying that the untransformed normal should be used as input into the texture matrix. The quick fix for this is to create a flexible vertex that has a position, normal and a three-element texture coordinate, and when the buffer is filled, you copy each normal vector into the texture coordinate. Unfortunately, this also increases the size of each vertex by 12 bytes and consumes more bandwidth when processing the buffer. (In a basic vertex case, these extra 12 bytes increases the vertex size by 50%.) But the cost is worth it: you can perform the "normal" spherical environment mapping (as used in the Direct3D sample) with a static vertex buffer, using nothing more than the standard Direct3D pipeline. This is a big win with hardware, since cards like nVidia's GeForce and GeForce2 process the texture matrix in hardware without CPU intervention, allowing the vertex buffer to be stored in local video memory.

Note that both the Direct3D and texture matrix examples expect a unit scale in the local-to-camera space transform (local*world). If this isn't the case, the texture matrix must be scaled by the inverse of the scale factor. Additionally, the normal-vector texture coordinates are expected to be of unit length. If this technique is applied to dynamic geometry, then every time a normal is modified, the associated texture coordinate needs to be updated. Another shortcoming of the method discussed above is that only the original input normal vectors are considered when calculating the reflection which for most meshes is fine but when mesh skinning is applied there is a problem. When skinning a mesh in hardware each vertex (position and normal) is multiplied by a pair of world transforms, the final position and normal is calculated from a weighting applied to the results of these transforms. This skinned normal and position is not available outside of the graphics pipeline but to obtain a correct reflection we need to know what the skinned normal vector was but we have a problem, one solution would be to use the CPU to reskin the mesh but this is expensive.

Rob Wyatt has been involved in games and graphics for more than a decade and was one of the architects of the X-Box game console, he recently left Microsoft and headed to Southern California where he can be found flying around the skies of Los Angeles in his plane. He is currently looking at various technologies for the Internet