Trending
Opinion: How will Project 2025 impact game developers?
The Heritage Foundation's manifesto for the possible next administration could do great harm to many, including large portions of the game development community.
Wang tiles are a simple and easy way to produce arbitrarily large procedurally generated game environments, from dungeons and caves to cities or wilderness. This tutorial covers the basics of their use, and how to ensure you get the same world every time.

Wang tiles are a simple and easy way to produce procedurally generated game environments, from dungeons and caves to cities or wilderness, but care must be taken if you need them to be consistent.
Wang tiles are regular tiles (typically square) the edges of which are assigned colours or styles from a limited set, and which can tile a plane when placed such that each edge of each tile is the same as the edge of the adjacent tile. To tile an infinite plane, one must assume that an infinite number of each tile within the set is available. This is not the case with physical board games, where Wang tiles are often used to great effect. In mathematics and formal logic, neither rotation or mirroring of the tiles are allowed, but it can be useful to relax this rule for procedural environment generation. Allowing for rotation and/or mirroring drastically reduces the number of tiles that need to created.
Wang tiles were first proposed by Hao Wang in the 1960's. They are most often studied because certain sets of Wang tiles can be shown to have no periodic (repeating) tiling over an infinite plane, which was first shown by Robert Berger in 1966. For this reason, they are sometimes used when texturing large surfaces, to avoid obvious repeating patterns. However, I wish to talk about their use in world generation, because they have one other interesting property that lends itself well to games: the ability to only place the tiles that you need, without having to tile a large area that the player may never visit.
Wang tiles allow for an arbitrary area to be tiled, but that area does not have to be rectangular, and it does not have to be tiled all at once. When the player reaches the edge of the explored space, you can simply place one or more new tiles down for them to explore. This allows the player to explore an effectively infinite space without having to generate or store terrain that never gets visited.
Environments created from Wang tiles often tend to appear naturalistic or sometimes haphazard, and thus are ideally suited for generating caves, dungeons, and mazes. One of their strongest advantages is that they often do not appear to be composed of tiles at all, since by definition, all the edges match with their neighbours.
Because the rules for placing them are quite simple, it is easy to understand or adapt the system to fit the needs of specific games. You can, for example, use Wang tiles for the world geometry, but bias the pseudo-random selection based on a noise function. Doing so could create regions where certain tiles were more or less prevalent, and help create a more cohesive feeling world.
In his papers on Herringbone Wang tiles, Sean Barrett points out the important distinction between what he calls a "complete stochastic set" and what I will call an incomplete set. A complete set of tiles is one that contains at least one tile for every possible combination of edge types. For example, for square tiles with just two types of edge, the complete stochastic set consists of 16 tiles, assuming the tiles cannot be rotated or mirrored; rising to 64 tiles with three different edge types, or 256 with four types of edges. While the number of tiles required to form a complete stochastic set increases dramatically as you add new types of edges, having a complete set reduces the impact individual tiles have on the overall pattern, because any single tile can only ever affect its immediate neighbours.
With an incomplete set, it is easy to end up in a situation where no tile fulfils the pattern of edges required by its neighbours. Having a complete stochastic set of tiles removes this concern and ensures that it is always possible to place a tile in any given location. It can also be noted that a complete set of tiles can include more than one tile for some, or all, combinations of edges, allowing increased variety and a larger pool of assets to draw from.
Typically, the mathematical and logical theories involving Wang tiles do not allow for rotation or mirroring since that will trivially allow for a periodic tiling to be possible with just a single tile. This rule can often be relaxed for games, however, where it is more important to have a complete stochastic set of tiles than it is to have no possible periodic tiling. Allowing for rotation and/or mirroring will very much depend on the game you are making, but can produce dramatic savings in the number of tiles you need to produce. In our game 31 Pixels Later, we managed to reduce the number of tiles needed from 256 tiles (4 sides with 4 types of edge) down to just 70 by allowing rotation. Were it not for the need for road markings to remain on the correct side of the street, we could have brought that number lower still by allowing for mirroring as well.
The process of placing new tiles into a Wang tiled environment is relatively simple. First the game looks at the already generated tiles adjacent to the position of the new tile. Each of these neighbouring tiles exerts a constraint that will limit the set of tiles available for that position. These constraints are used to filter down the complete set of tiles to only those that are suitable. Finally, one of these is selected at random, and placed into the world.
For the examples in this article I will stick with a very simple set of just 16 tiles. Each tile has 4 edges, and has just two types of edge: grass or road surface. For clarity, I will disallow rotation and mirroring, which produces a complete stochastic set consisting of 42 = 16 tiles (four edges from 2 possibilities per edge). The complete tile set it shown below.

Tile graphics are taken from the excellent Kenney Isometric Landscape tile pack, which is available under a CC0 public domain license.
At the start of the game, pick a single tile and place the player upon it. Depending on the type of game you're making, you might want to pick something totally at random, or pick from a shorter list of tiles that make for good starting locations. I'm going to arbitrarily pick the crossroads tile to start from. Because crossroads have been mysterious and mystical ever since mankind first started building roads, and because they make good starting points for exploration, conveying a sense that the player can explore in any direction they like.
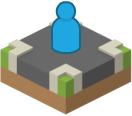
Player token also by Kenney, from the Boardgame Pack, licensed CC0 public domain.
At this point it is up to the player to decide which direction they want to explore. For this example, I'll have them move up and to the right, which I shall henceforth call north. Because they are walking off the edge of the explored map, the generator must be executed to decide the next tile.
The first step is to look at the neighbours of the new tile, and work out what the edge constraints are. In this case, it only has one neighbour (the crossroads they started on), and so it has a single edge constraint of "south: road". Filtering the list of tiles to just those which match the constraints gives the following 8 tiles.

The new tile must be one which has a matching edge.
From that reduced set of tiles, the generator picks one of the tiles at random and places it into the world (for this example, it picked the 4th tile, the curved road), as shown below.
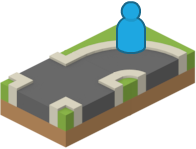
After the first move.
Once the player has dealt with whatever challenges might be on the new tile, they have a choice, to either move back the way they came, or to explore in one of the other directions and expand the world again. For this example, the player will follow the road east. Begin by examining the 4 neighbours of the tile that they are attempting to move into, and work out the edge constraints. In this case, there is only one neighbour (the curved road) which makes for a single edge constraint of "west: road". Filtering the complete tile set to just ones with roads on the west edge gives the following set of tiles.

Filtering the tile set down to just those which have a road as their western edge.
From the reduced set of tiles, the generator picks one at random and adds it to the world map. For this example, it will pick the second tile, the straight road, as shown below.
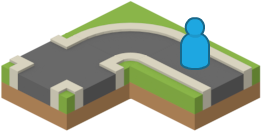
After the second move.
Now the player gets to explore the straight road, and decide where to move next. This time I will have them leave the road and head south. As before, the terrain generator must examine the four neighbours of the tile they are moving into. Unlike before, there are now two neighbours: the straight road they have just left, and the crossroads where they began the game. These exert two constraints, and the selected tile must conform to both "west: road" and "north: grass".

The complete tile set is filtered down to ever-smaller sub-sets as more constraints are applied by the need to match edges with neighbouring tiles.
From the limited set of tiles I am using for these examples, there are just four tiles which match both constraints imposed by the neighbouring tiles. Note that if there were four neighbours already placed (by the player having walked in a large circle and deciding to step into the middle), there would only be one tile that could fit, and the generator would have to randomly select from a list of one tile. It is for this reason that games using Wang tiles for terrain generation must usually ensure they have a complete stochastic set of tiles, or else they run the risk of having the player move into a part of the map that cannot exist, because no tile matches the constraints of its neighbouring edges.
In physical board games that rely on players building a world out of Wang tiles, you often come across the situation where there are spaces where no tile can possibly fit. Even if the game has a complete stochastic set of tiles, physical games by their nature have a finite quantity of each type of tile, and cannot just produce a new instance when needed in the way computer games can. When playing board games however, players are much more aware of the rules of the system, and these situations are less immersion breaking than they would be in a video game, where a missing tile could cause the player to fall through the world, or cause the game to crash entirely.
If the generator randomly selects the third tile from the filtered set above (the curved road corner) and adds it to the world, the game world would look as follows.

After the third move.
While the approach outlined above can and does work well, it is limited by one key factor which may not be immediately obvious — the player shapes the world around them.
Normally when people think about exploring an environment, in video games or in real life, they start out with a limited knowledge of what is around them, and build up a mental map as they discover new areas, but those areas are fixed in place before they are discovered, and do not change merely by the act of being observed. That is not what is happening here, and I don't just mean in a technical sense, but a very real way.
In the previous example, each time the player moves off into the unknown, the game generated a new tile for them to explore. If the camera was set up to look down upon the player, and the new tile was generated when they got close to the edge of the old one, then the player might not even realise that the world is made up of tiles, and might think they are exploring a continuous world. Each tile however, was picked from a set determined by the edges of the neighbouring tiles, and thus the order in which the player explores the world, shapes the world they are exploring.
Had the player gone a different way, the world they would have experienced would have been different, even if the random number generator was given the same seed value to start with, as shown by the following example.

Crossroads trivia: The Roman goddess Trivia was said to haunt crossroads, much as her Greek counterpart Hecate did. They were both also associated with witchcraft and the spirits of the dead.
As before, the game begins with the player standing at a crossroads, however this time, they will head east initially. That tile does not yet exist, and has only one neighbour, exerting a constraint of "west: road", which results in a different set of filtered tiles than the "south: road" constraint did in the original example.

If the player went east initially, they would see a different world than had they gone north.
A Pseudo-Random Number Generator (or PRNG) is used to select from the filtered set of tiles each move. I will talk about them in more detail later on, but for this example it is important to note that PRNGs generate a sequence of numbered based on an initial state (or seed). Because the PRNG was seeded with the same starting value as in the previous example, it will produce the same sequence of numbers as it did previously: 4, then 2, then 3. The fourth tile from the filtered set is selected, which is a different curved road section to that chosen for the first move in the original example.
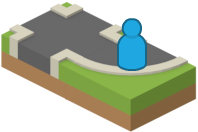
Starting from the same seed, exploring a different way produces a different environment.
From this point, the player follows the road to the north. This tile does not yet exist and has one neighbour, which exerts the single constraint of "south: road".

The set of tiles with a road at their southern edge.
The second value the pseudo-random number generator will produce from this seed is 2, and so the second tile in the filtered set, a straight road, gets added to the world, as shown below.
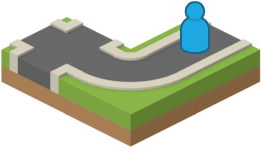
After the second move.
Finally, the player moves west, and a new tile must be selected that conforms to the two constraints imposed by its neighbours ("south: road" and "east: grass").

The set of tiles having both a road at the southern edge and grass to the eastern edge.
The random generator picks the third tile, a curved road, and adds it to the world. As you can see, the world generated by this route is quite different from the one produced in the last example.
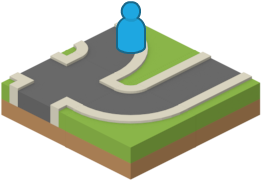
After the third move.
While the approach taken so far works well and will often be satisfactory for many games, there are several advantages to having a world generator that can produce consistent results. A consistent generator is one that when given a single starting seed value, will reliably and repeatedly produce the same world, regardless of player action or order of exploration.
The first and most obvious advantage is re-playability and competition for high scores. While watching groups of people play my game 31 Pixels Later, I inevitably see them try to compete for high scores, and this has in turn drawn them back to play again when their score gets beaten. For 64 Pixels Later, I wanted to implement a consistent world generator and online high score tables to enable players to not only compare scores based on random levels, but also compete on the exact same level, to see who could score highest on it. Having a consistent world generator also allows for daily and weekly levels in which players worldwide can all compete on the same level.
It can also ease network and storage requirements, since the game does not need to store or transmit the complete state of the world. The game can simply remove explored areas from memory when the player moves on, because they can easily be re-created as needed, if and when the player returns that way. If the player makes any changes to the world (killing monsters, blowing up buildings, or even building structures of their own) then only these changes need to be saved, and not the entire state of the tile.
Some games use consistent procedural generators, but lock them down to specific seeds for some, or all, of the time. This creates static areas that are the same for all players allowing for a sense of continuity and community, and allows the developer to set up fixed narrative elements in specific areas, while still allowing for a potentially infinite landscape to explore. The areas or levels with fixed seeds can be left as they are or modified by hand by a level designer, with only the changes from the generated original needing to be stored.
In the two previous examples, I used a Pseudo-Random Number Generator (PRNG) that gave a consistent sequence of values over time, such that in both examples, it picked the 4th tile for the first move, then the 2nd tile for the second move, and the 3rd tile for the third move. This is because PRNGs typically use the last value they generated as the basis for the next value they will generate, with the very first value they produce being based on an external input called a seed value.

A Pseudo-Random Number Generator typically takes its last output as the input for the next operation, generating a repeatable sequence from each seed value given.
The obvious first step in getting a consistent world is therefore to bake the coordinates of each tile into the PRNG somehow, such that for every given location, the same value will be generated regardless of when it is visited. The easiest way to do that is to supply it with a new seed value for each tile generated, which is based on the coordinates of the tile, as well as the global seed value for the level. This is best achieved with a simple hashing algorithm, such as x + y * 255.

Re-seeding the PRNG before generating each tile, incorporating the coordinates of the tile plus the global seed value to calculate the seed for each tile, independent of previously generated values.
This will ensure that the random values picked for each tile are consistent and do not depend on any previously generated random values. However, given that each tile is still constrained to match the edges of the neighbouring tiles, the set of tiles from which to randomly select still varies depending on the order of exploration.
In order to generate a consistent world regardless of the order of exploration, it is important to remove the influence existing tiles have on the generation of new tiles. The only way to select a Wang tile that is not based on any of its neighbours is to generate new tiles only in locations that have no neighbours, since those tiles would have nothing to be influence them except for the PRNG. If the PRNG is re-seeded based on map coordinates, then every tile generated that has no neighbours will be generated in a consistent way.
A world in which no tile can sit next to another tile would not be very interesting since it would only be possible to have isolated single tiles. Hence, the remaining tiles still need to be generated in a manner that is influenced by the existing tiles, but which is not dependent on the order of exploration. The way to achieve that is to only generate tiles which have either no neighbours already generated or have all their neighbours already generated.
For grids of square tiles, it helps to think of a checkerboard where the white tiles are always generated before any of their neighbouring black tiles, and where the black tiles can only be generated after all four neighbouring white tiles. If the player tries to move into a black tile, the game must first generate any missing white neighbours, and they are guaranteed (if the rule has been followed) to not have any of their neighbours already generated.

Each white tile must be generated before any of its black neighbours, while the black tiles may only be generated after all four white neighbours are generated.
The very first tile generated using this system clearly has no neighbours (because it is the first tile), and thus is a white tile, with its immediate neighbours being black tiles.
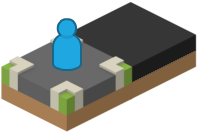
The first tile generated has no neighbours, making it white. The neighbouring tiles will all be black.
If the player then moves north, the game would have to generate the next tile for them. However, being a black tile, it cannot be generated until all four neighbouring white tiles are generated. At this point only one of the white neighbouring tiles has been generated (the crossroads the player just moved away from).
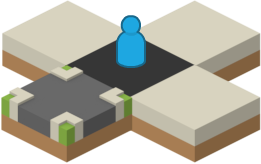
When the player moves onto a black tile, all neighbouring white tiles must be generated first.
White tiles can be generated in any order, since they can never be neighbours and thus will not influence each other. So long as the pseudo-random number generator is re-seeded based on their coordinates, their coordinates are the only source of influence over the selection of the white tiles. Depending on the type of game, the contents of these tiles might need to be obscured from the player, as they have not been visited by the player yet.
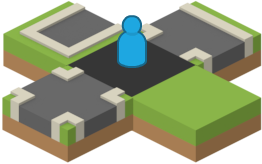
White tiles can be generated in any order, as they do not have any neighbours to affect their generation.
Finally, once all four of the neighbouring white tiles have been generated, the black tile the player moved onto can be generated. There are now four constraints imposed by the surrounding tiles ("north: road", "south: road", "east: grass", and "west: grass"). In the tile-set I am using in these examples, there is only one tile that fits these constraints: a straight road from north to south.
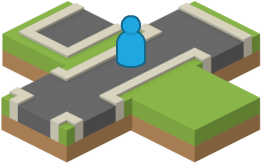
Black tiles can only be generated after all of their neighbours have been generated.
So far, I have only provided examples using a regular grid of square tiles, as this is the most common scenario. The techniques can be applied to other tiling patterns as well, although possibly with the addition of intervening steps.
Triangular grids, both right angled and equilateral, can follow the same rules as forsquare tiles, since the grid can be coloured regularly with just two colours, white (no neighbours) and black (all neighbours). As before, if the player moves into a black tile, all of its white neighbours must be generated before it can be.
For Hexagonal grids, and most grids composed of more than one shape of tiles, things become more complicated. One or two additional colours are required to ensure that neighbouring tiles do not share colours. To achieve this, the grid that is either coloured white, grey, and black (as shown in the example below) or coloured white, light grey, dark grey, and black.

For hexagonal or mixed-shape tiling, a regular repeating pattern of between two and four colours must be found, such that no tile is the same colour as their neighbours. These tiles are modified from ones in the Hexagon Tiles pack by Kenney, licensed CC0 public domain.
As before, white tiles are generated first, when they have zero neighbours already generated, and black tiles can only be generated after all six neighbouring tiles have been generated. The grey tiles can only be generated after their white neighbours but before their black neighbours.
The first tile generated has no neighbours, and is considered white. The tiles around it, following the pattern defined above, are a mixture of black and grey. In this example, I will show what happens when the player attempts to explore one of the black tiles next to the starting tile.
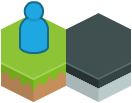
The first tile generated is always a white tile, since it is generated without any neighbours exerting constraints over it.
If the player attempts to explore a black tile, all six of the surrounding tiles must be generated first. The two white tiles can be generated immediately, and in any order since they have no neighbours to influence them.
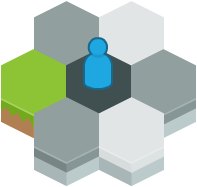
Before any black tile can be generated, all six of the surrounding tiles must be generated.
The white tiles, having no neighbours, are simply selected at random from the set of all available tiles. The grey tiles however can only be generated once all three of their white neighbours have been generated.
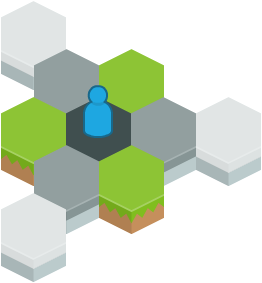
White tiles should be generated as soon as needed, but grey tiles can only be generated after all three white neighbours have been generated.
These white tiles are also simply picked at random from the complete set of tiles, because none of their neighbouring tiles have been generated yet. As with the previous examples, this means they are only influenced by the pseudo-random number generator.
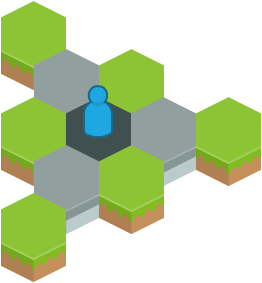
Grey tiles may only be generated once all three of their white neighbours have been generated.
Once all three white tiles are in place around each grey tile, the grey tiles themselves can be generated. Each is selected by first reducing the set of all available tiles down to only those which match the three edge constraints imposed by its three white neighbours, and then randomly selecting a tile from that reduced set.

Black tiles can only be generated once all six neighbouring tiles have been generated.
Finally, now that all six of its neighbours have been generated, the black tile the player moved onto can be generated. The tile is selected from the reduced set of tiles which conform to all six edge constraints imposed by the six neighbouring tiles. Often this will only leave one or two tiles to randomly select between. Once again, depending on the nature of the game, the other tiles which have been generated but not explored yet may need to be hidden from the player.

The state of the world after a single player movement.
It is my hope that this guide has helped you to better understand the value of Wang tiles for generating environments in your games. Wang tiles are an excellent tool for procedurally generating arbitrarily large environments, both natural and constructed. The ability to only generate the parts of the world as they are needed leads to efficient generation, while the simplicity of the rules governing world generation make them easy to understand and implement. The simplicity of the rules also allows for additional layers of procedural generation to be added to create environments with larger scale structure and thematic consistency.
I hope also to have provided a simple and easy to understand set of rules that should ensure your Wang tiled environments remain consistent over multiple games and allow you to reduce the burdens on level storage and network transmission. While not essential for every game, I believe every game can benefit from the added security of knowing that the world is based on a single seed, rather than having the world vary depending on the order in which it is explored.
The techniques for consistent world generation were developed while writing my upcoming game, 64 Pixels Later, which is currently on Steam Greenlight. Please consider supporting me by clicking here and giving me a "yes" vote.
Thank you.
Nick Turner.
Read more about:
BlogsYou May Also Like