What game devs can learn from Japan's most interesting puzzle magazine

Nikoli (or “Puzzle Communication Nikoli”) is a Japanese puzzle company and magazine publisher best known for popularizing the type of logic puzzle they called Sudoku.

Devs who aren't familiar with Nikoli should be, as the company has been making headway with more puzzles of that style: symbol-based logic puzzles that are more accessible than crosswords (since players need only read numbers and icons) where the player is presented with a diagram containing clues, and must complete the diagram by filling it with lines or symbols according to those clues.

Learning about these puzzles, and how to solve them is of immense value for puzzle-making game designers. Being familiar with this style has much to teach about both the nature of puzzles, and what it is about puzzles that makes them enjoyable: the joy of applying reason, knowledge and skill to solve a difficult problem.

In designing video games, many of these puzzles can be adapted as minigames, with the marks of a pencil replaced with the movements of a character. Further, studying these puzzle types is of use in presenting, to players, problems that are just difficult enough.

This is valuable because it's often hard to gauge, when designing a game or puzzle, whether the thing you're making is too easy or hard. There’s a somewhat standard way to determine the difficulty of a Nikoli, or symbol-based logic, puzzle: is it possible to solve it without resorting, at some point, to “trial and error?”

The appeal of a Nikoli puzzle

Here I present an introduction to the style, and I take one type of Nikoli puzzles, called “Slitherlink” also known as Loopy, and work through some tricks to solving them. Then I step back a bit, and look at the process of creating Slitherlink puzzles themselves, which is made easier once you’ve figured out how to solve them. Then, at last, I take a few more steps back, and try to give you some insight into going beyond that, making new puzzles of one of the pre-existing types.

Nikoli president Maki Kaji demonstrating puzzles during New York's Sakura Matsuri festival

While these puzzles may vary considerably in style, they all have certain facts in common. First, they all have exactly one solution, which can be figured out through logical deduction from the clues given. Second, unlike “cultural” puzzles like crosswords, none require outside knowledge (other than of the basic rules) to complete. Arithmetic is not required either, even though some puzzles involve numbers. As in Sudoku, some puzzles that involve numbers use them simply as symbols, divorced from their numeric meaning, but some of them do use them for their values.

I’m calling these puzzles Nikoli puzzles, even though some of the type were not invented by them. It’s just a useful term. Intriguingly, the process of learning how to solve them is its own puzzle. I have found satisfaction in the process of taking a type of Nikoli puzzle I had never encountered before and, from its rules, figuring out how to solve them. Like with Sudoku, the easiest puzzles of a type tend to be solvable with little more than simple insights; the hardest ones may be so difficult that, even with lots of tricks, they may not be solvable without some trial and error.

That isn’t to say that insight, which amounts to solver-discovered algorithms, is useless with those puzzles; on the contrary, they can be extremely useful in taking a formidable puzzle and reducing it to a level where a small number of solutions are left, within reach for a determined solver.

Because of the joy of learning how to do a new style of symbol logic puzzle, I don’t really want to give away too much about any one type of puzzle. However, someone entirely unfamiliar with them, other than maybe Sudoku (which used to be ubiquitous and is still pretty common), might be lost as to how to even get started in this process. So, let’s step not just step through how to solve one Slitherlink puzzle; let’s see what we can figure out about this style of puzzle in general.

Challenge design the Slitherlink way

A Slitherlink puzzle is a grid of dots with numbers written in amidst them. The dots form a square grid, and the numbers are always in the cells of that grid.

The solver’s job is to draw in lines between the dots, along the edges of each cell, in such a way that numbered cells have that many lines bordering them. An additional complication is, all the lines in total, throughout the whole puzzle, form a single continuous loop with no branches or extra lines.

As mentioned above, a properly-designed Slitherlink puzzle has only one possible solution. I’ve provided an example of one here (generated by Simon Tatham’s Puzzle Collection).

A Slitherlink puzzle

The solution to the puzzle. Notice, each number has exactly that many line segments bordering it

The specifics vary a lot, but the basic process for solving all Nikoli puzzles is the same:

Step 1: Find the places that are easily completable, and complete them.

Step 2: Use that information to help you figure out the next places that are trivial to complete. Keep doing this until you run out of simple-to-do places. With very easy puzzles, that may be enough to solve the whole thing.

Step 3: When all the obvious cases are exhausted, use higher-level insights to reason through as much of the rest of the puzzle as you can do. These are “tricks,” consequences of the rules that are not immediately obvious. I describe a few of those below. This is enough to take care of intermediate-level puzzles.

Step 4: In difficult puzzles, you’ll eventually reach a place where all tricks fail you. This is where what is called “trial and error” is required: one looks at the puzzle and makes a guess about a move, then works out the consequences of that move.

Paradoxically, when doing this it is usually better to make a bad guess, an impossible move that turns out to break one of the puzzle’s rules, than a good one. If you find out that your guess results in an illegal solution, then, because there is only one possible legal solution to the puzzle, you know that the reverse of your guess must be part of the solution.

To use Slitherlink as an example, if you draw a line, then find out that the line cannot join up with the other lines to form a single continuous loop, then your guess must be incorrect, and you can mark an X in the spot where the guessed line was. Knowing there cannot be a line there might be enough to allow you to continue using the other methods to solve the puzzle, or you might run out of steam again, and have to make another guess.

This also works the other way: your guess could be placing an X, and if its consequences would put the puzzle into an illegal state, you know a line there is part of the solution.

So what if the guess turns out to be “good?” If it means you the player can work through the entire rest of the puzzle and reach the sole solution, then that’s great, over and done. But usually what happens is, the guess doesn’t let you finish the whole puzzle, and you get stuck again. That’s the worst-case scenario: you actually don’t know, in that event, if your guess was good or bad, and you must erase all the progress you made from the guess. You also must erase all the progress resulting from a guess if you reached a contradiction, but at least then you got something out of it.

Because of all that erasing, it’s best, if trial and error turn out to be necessary to solve, to work from a copy of the puzzle so as to not tear up the paper too much. Computer puzzle collections have a great advantage here, since most of them let you rewind puzzle state indefinitely with the simple press of an Undo key.

Step 5: The very hardest puzzles can go even beyond that. It might be the case that all the single-move guesses you could make are inconclusive. Then you’d have to resort to multi-step trial and error, where you make two guesses. Then, if you reach a contradiction, it’s still possible that one of the guesses is correct and the other is wrong.

Solving one of those is terrifically taxing, but it’s possible. You could go even farther, if you try all the possible two-guess combinations, but now we’re reaching the domain of extraordinarily difficult challenges, and I must abandon you to your own efforts there.

Let us return to the case of Slitherlink.

Slitherlink Tricks, and Their Discovery

I mentioned that discovering tricks to a Nikoli-style logic puzzle amounts to a puzzle in itself. Let’s step through some simple tricks.

Since the solution is a continual loop, without branches or isolated lines, when the line goes through a corner, any other possible connections to that corner must be empty. This is on of those things that seems obvious at a glance, but turns out to have interesting consequences.

There can be no “4” hints in the puzzle. A hint of 4 would fill all sides of a square, making a complete loop to itself. Unless that were the whole (extremely easy) puzzle, there could be no other lines to fill in. Thus, you’ll never find a hint of 4 anywhere in a Slitherlink puzzle.

“0”s are disruptive. Since a 0 hint means no adjacent lines can be marked, it makes quite a gap. Note, however, that 0s say nothing about whether the loop touches any of that square’s corners, only its sides.

There are only four possible arrangements for lines around each “1” and “3,” and only six around a “2.” A 3 hint must be a sequence of three adjacent lines, making a kind of “bump” in the loop. And a 1 can only host one adjacent line, with the other three empty just like a 0. 2s are the most complex case. There are six possible lines around a 2, and so 2 hints, by being the least restrictive, likewise tell us the least about the solution. They do tell us something, but fields of 2s usually require other numbers, nearby, to reveal anything useful.

Now that we’ve looked at these cases, we can start to think about them in relation to each other. For example, the only way there can be adjacent 3s is when the loop threads between them. Take the situation where the “empty” side of a 3 is on the same side as the other 3. The only way they could legally be placed there is if there were a complete loop around them, which would forbid any other lines in the puzzle. So, in this situation, the loop must thread between them. There can be more 3s in a row, as well, and no matter how many they are, the line must keep threading between them.

That also means that the line between them, and on either side, must be filled. So, at a glance, any time you spot adjacent 3s in the puzzle, you can fill those lines in. In cases where there’s more 3s, you can keep drawing lines.

Horizontal or vertical chains of 3s must be separated by lines

Also, when two 3s are diagonally-adjacent, the outermost “bracketing” lines must be filled. It takes a little more thought to see why this is so. It’s a consequence of Observations 1 and 4. When the line comes to a “3” square, it must wind around three of its corners. If one of these bracketing lines were empty, the other three would have to be full, which would in turn mean two of the other three’s sides would have to be empty.

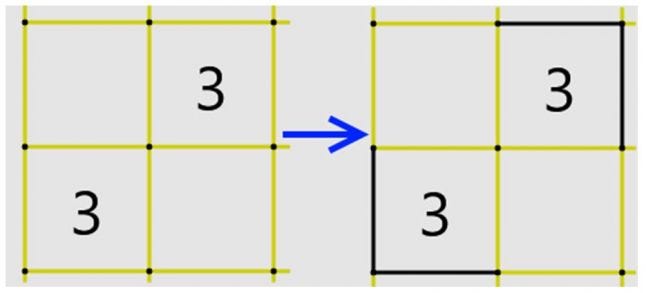
Diagonal pairs of 3s must be bracketed by lines, like this

Since the loop must not have any branches, every time the loop goes through a corner, either straight or making a turn, the routes it didn’t take must be empty. This may be obvious, but when you go through and mark out all the dead lines a partial solution leaves, you might be surprised as how much simpler the puzzle looks!

Almost every time you draw a line longer than one segment, you also reveal lines that can’t be in the solution.

There’s more such rules to discover. Try to figure out the further implications yourself, for it’s part of the joy of Nikoli-style logic puzzles. For example, what can we deduce about diagonally-adjacent 3s? What would happen in the event of a chain of diagonal 3s? Is such an arrangement even possible? What, if anything, can we determine about a 3 and a 1 touching orthogonally? Diagonally? Is there potentially anything special about diagonal chains of 2s?

Here’s a few other examples of Nikoli-style puzzles:

Gokigen Naname (or “Slant”) puzzles are kind of the inverse of Slitherlink. You draw diagonal lines across grid squares, the numbers indicate how many lines connect to them, and the solution will have no loops

Hashi (aka Bridges) adds some extra uncertainty to the mix. Each digit represents the number of lines that connect it to other numbers. All lines must be straight, either horizontal or vertical, and cannot cross any other lines or digits. Importantly, each “bridge” can either consist of one or two lines. When complete, all the digits and lines will form one continuous structure; there will be no isolated “islands” that cannot be reached

Creating a Nikoli Puzzle

Here things start to get more complex. While I cannot offer hard-and-fast rules for puzzle creation, I can offer this advice.

Creating a Nikoli-style logic puzzle is not as difficult, I would say, as creating a crossword puzzle, which usually takes either considerable trial-and-error effort or the aid of a computer program to generate a good “fill,” and even after that, one must write fair clues. The fill portion is particularly difficult, especially if you’re doing it to American publishing standards.

The better you are at solving a class of Nikoli puzzle, the better you will be at creating them. Since you know the tricks to constructing the puzzle, you can use those to help give the solver just enough help to deduce the solution.

The primary tactic is to start with the solution and work backwards. In the case of a Slitherlink puzzle, start with a legal solution drawn on an empty grid. Make a copy of this solution. Then go step by step. Find places where the loop matches some of the tricks you’ve learned in solving. If you’ve found a couple of spaces where there would be 3s arranged diagonally, for instance, write in those 3s on the grid, then erase the “brackets” around them. If there are 3s in those places, then those lines can only be filled.

After you’ve filled in a few places like that, you can work outwards from there, filling in numbers and erasing the lines that they imply. Keep going until the whole loop is erased, and you have a Slitherlink puzzle!

Well, for the most part. If you work entirely like that you’ll be certain to have a workable puzzle, but if algorithm tricks can get you the entire way it probably won’t be very difficult to an experienced solver. The hardest puzzles, the ones that require greater insight, and perhaps trial-and-error, to solve, it can help to proceed in a similar kind of way. Make a copy of a blank grid with your essential, trick-derived numbers filled in, and then fill in a couple more numbers, using your solution.

From there, try to work through the puzzle in different ways, and see if the numbers make your solution definite, or if they allow too much leeway and make another solution possible. Experience, both in solving puzzles and in making them, is you ally here.

Finally, there is the excellent open source software Simon Tatham’s Puzzle Collection, which contains random generators for many kinds of Nikoli-published puzzles, and quite a few other logic puzzles besides.

Since the source code is available, you may be able to use it to figure out how to implement your own algorithm. It is made available under the MIT license, fairly permissive terms, which has resulted in a proliferation of mobile adaptions of the collection.

Creating a Nikoli-style puzzle type

If creating a puzzle of one of Nikoli’s styles isn’t difficult enough, creating a new class of Nikoli puzzle is more challenging still. Learning about puzzles in general, and the different kinds of Nikoli puzzles in specific, will help, but this is essentially a creative enterprise, and hard-and-fast rules can only carry us so far.

I tried constructing a set of Nikoli-style puzzle rules on a whim for this article, and made some progress, but ultimately failed. It’s not as easy as you might think. Special care must be taken to guard against alternate solutions. In most cases, a beginning constructor must first be an experienced solver, and so I direct a novice’s attention there.

Other sources

Does Slitherlink sound interesting to you? A Slitherlink collection is available for Nintendo 3DS on the eShop, and of course Simon Tatham’s Puzzle Collection will create an endless supply for you for free. With the right command line parameters, it’ll even generate printable puzzle and solution sheets. It is available for many platforms. By the way, all the illustrations in this article got their start from STPC screenshots.

You can find out more about these symbol logic puzzles from this Online Puzzle Encyclopedia. Nikoli also publishes constructor-made puzzles on the web, some that can be played for free. And Hudson/Konami released a 3DS cart with four puzzle styles on it (including Sudoku), called Nikoli Puzzle Collection. It tends to be available very cheaply in used game stores; I got my copy for about $4, and have found it to be well worth that price.