Modeling for computer games addresses a wide range of problems and has evolved over the years, but the computer graphics modeling pyramid has yet to have a substantive apex. Going beyond geometric, kinematic, physical, and even behavioral models, John Funge talks about the myriad of possibilities inherent to cognitive models.
Modeling for computer games addresses the challenge of automating a variety of difficult development tasks. An early milestone was the combination of geometric models and inverse kinematics to simplify keyframing. Physical models for animating particles, rigid bodies, deformable solids, fluids, and gases have offered the means to generate copious quantities of realistic motion through dynamic simulation. Biomechanical modeling employs simulated physics to automate the lifelike animation of animals with internal muscle actuators. Research in behavioral modeling is making progress towards self-animating characters that react appropriately to perceived environmental stimuli. It has remained difficult, however, to instruct these autonomous characters so that they satisfy the programmer's goals. Hitherto absent in this context has been a substantive apex to the computer graphics modeling pyramid (Figure 1), which we identify as cognitive modeling.
Cognitive models go beyond behavioral models, in that they govern what a character knows, how that knowledge is acquired, and how it can be used to plan actions. Cognitive models are applicable to instructing the new breed of highly autonomous, quasi-intelligent characters that are beginning to find use in interactive computer games. Moreover, cognitive models can play subsidiary roles in controlling cinematography and lighting. See the color plates at the end of this article for some screenshots from two cognitive modeling applications.
We decompose cognitive modeling into two related sub-tasks: domain knowledge specification and character instruction. This is reminiscent of the classic dictum from the field of artificial intelligence (AI) that tries to promote modularity of design by separating out knowledge from control.
knowledge + instruction = intelligent behavior
Domain (knowledge) specification involves administering knowledge to the character about its world and how that world can change. Character instruction involves telling the character to try to behave in a certain way within its world in order to achieve specific goals. Like other advanced modeling tasks, both of these steps can be fraught with difficulty unless developers are given the right tools for the job.
Background
The situation calculus is the mathematical logic notation we will be using and it has many advantages in terms of clarity and being implementation agnostic, but it is somewhat of a departure from the repertoire of mathematical tools commonly used in computer graphics. We shall therefore overview in this section the salient points of the situation calculus, whose details are well-documented in the book [Funge99] and elsewhere [LRLLS97,LLR99]. It is also worth mentioning that from a user's point of view the underlying theory can be hidden. In particular, a user is not required to type in axioms written in first-order mathematical logic. In particular, we have developed an intuitive high-level interaction language CML (Cognitive Modeling Language) whose syntax employs descriptive keywords, but which has a clear and precise mapping to the underlying formalism (see the book [Funge99], or website www.cs.toronto.edu/~funge, for more details ).
The situation calculus is an AI formalism for describing changing worlds using sorted first-order logic. A situation is a "snapshot" of the state of the world. A domain-independent constant s0 denotes the initial situation. Any property of the world that can change over time is known as a fluent. A fluent is a function, or relation, with a situation term (by convention) as its last argument. For example, Broken(x, s) is a fluent that keeps track of whether an object x is broken in a situation s.
Primitive actions are the fundamental instrument of change in our ontology. The sometimes counter-intuitive term "primitive" serves only to distinguish certain atomic actions from the "complex", compound actions that we will defined earlier. The situation s' resulting from doing action a in situation s is given by the distinguished function do, so that s' = do(a,s). The possibility of performing action a in situation s is denoted by a distinguished predicate Poss (a,s). Sentences that specify what the state of the world must be before performing some action are known as precondition axioms. For example, it is possible to drop an object x in a situation s, if and only if a character is holding it:
The effects of an action are given by effect axioms. They give necessary conditions for a fluent to take on a given value after performing an action. For example, the effect of dropping a fragile object x is that the object ends up being broken
Surprisingly, a naive translation of effect axioms into the situation calculus does not give the expected results. In particular, stating what does not change when an action is performed is problematic. This is called the "frame problem" in AI. That is, a character must consider whether dropping a cup, for instance, results in, say, a vase turning into a bird and flying about the room. For mindless animated characters, this can all be taken care of implicitly by the programmer's common sense. We need to give our thinking characters this same common sense. They need to be told that they should assume things stay the same unless they know otherwise. Once characters in virtual worlds start thinking for themselves, they too will have to tackle the frame problem. The frame problem has been a major reason why approaches like ours have not previously been used in computer animation or until recently in robotics. Fortunately, the frame problem can be solved provided characters represent their knowledge with the assumption that effect axioms enumerate all the possible ways that the world can change. This so-called closed world assumption provides the justification for replacing the effect axioms with successor state axioms. For example, the following successor state axiom says that, provided the action is possible, then a character is holding an object if and only if it just picked up the object or it was holding the object before and it did not just drop the object:
. 
Character Instruction
We distinguish two broad possibilities for instructing a character on how to behave: predefined behavior and goal-directed behavior. Of course, in some sense, all of a character's behavior is defined in advance by the animator/programmer. Therefore, to be more precise, the distinction between predefined and goal-directed behavior is based on whether the character can nondeterministically select actions or not.
What we mean by nondeterministic action selection is that whenever a character chooses an action it also remembers the other choices it could have made. If, after thinking about the choices it did make, the character realizes that the resulting sequence of actions will not result in a desirable outcome, then it can go back and consider any of the alternative sequence of actions that would have resulted from a different set of choices. It is free to do this until it either finds a suitable action sequence, or exhausts all the (possibly exponential number of) possibilities.
A character that can nondeterministically select actions is usually a lot easier to instruct, but has a slower response time. In particular, we can tell a cognitive character what constitutes a "desirable outcome" by giving it goals, and it can then use its background domain knowledge to figure out whether it believes a given action sequence will achieve those goals or not. Although we are using the word "nondeterministic" in a precise technical sense, the trade-off between execution speed and programming effort should already be a familiar and intuitive concept for many readers.
A third possibility we will consider is something of a compromise between the two extremes of predefined and goal-directed behavior. In particular, we introduce the notion of complex actions and explain how they can be used to provide goals, and a "sketch plan" for how to achieve those goals.
Before we continue, it is worth pointing out that sometimes people identify a particular class of programming languages with a particular kind of behavior. For example, logic programming languages are often associated with nondeterministic goal-directed behavior, and regular imperative languages with deterministic predefined behavior. While it is true that logic programming languages have built-in support for nondeterministic programming, there is nothing to stop us implementing either kind of behavior in any programming language we choose (assuming it is Turing complete). To avoid unnecessary confusion, we shall not tie the following discussion to any particular programming languages.
Predefined Behavior
There are many convenient techniques we can use to predefine a character's behavior. In this article, however, we are more interested in techniques for which the character's behavior is not completely determined in advance. Therefore, we shall not attempt a comprehensive survey of techniques for predefining behavior. Instead, we shall take a brief look at two particularly popular approaches: reactive behavior rules, and hierarchical finite-state machines (HFSM).
Reactive Behavior Rules
We will use the term reactive behavior when a character's behavior is based solely on its perception of the current situation. What we mean by this is that the character has no memory of previous situations it has encountered. In particular, there is no representation of its own internal state and so it will always react in the same way to the same input stimuli, regardless of the order in which the inputs are received. A simple way to encode reactive behavior is as a set of stimulus-response rules. This has a number of important advantages:
Although the set of rules might be short, and each of the rules very simple, that doesn't necessarily mean the behavior that results from the character following the rules is simple at all. That is, we can often capture extremely sophisticated behavior with some simple rules.
We can usually evaluate the rules extremely quickly so there should be no problem obtaining real-time response from our characters.
There is no need to worry about various knowledge representation issues that arise when characters start thinking for themselves. That is, the characters are not doing any thinking for themselves; we have done it all for them, in advance.
The use of reactive behavior rules was also one of the first approaches proposed for generating character behaviors, and it is still one of the most popular and commonplace techniques. Great success has been obtained in developing rule sets for various kinds of behavior, such as flocking and collision avoidance. As an example of a simple stimulus-response rule that can result in extremely sophisticated behavior, consider the following rule:
Believe it or not, this simple "left-hand rule" will let a character find its way through a maze. It is an excellent example of how one simple little rule can be used to generate highly complex behavior. The character that follows this rule doesn't need to know it is in a maze, or that it is trying to get out. It blindly follows the rule and the maze-solving ability simply "emerges". Someone else did all the thinking about the problem in advance and managed to boil the solution down to one simple instruction that can be executed mindlessly. This example also shows how difficult thinking up these simple sets of reactive behavior rules can be. In particular, it is hard to imagine being the one who thought this rule up in the first place, and it even requires some effort to convince oneself that it works.
We can thus see that despite some of the advantages, there are also some serious drawbacks to using sets of reactive behavior rules:
The biggest problem is thinking up the correct set of rules that leads to the behavior we want. It can require enormous ingenuity to think of the right set of rules and this can be followed by hours of tweaking parameters to get things exactly right.
The difficult and laborious process of generating the rules will often have to be repeated, at least in part, every time we want to effect even a slight change in the resulting behavior.
Since the behavior rules are deterministic, once an action is chosen, there is no way to reconsider the choice. There are many cases when a cognitive character could use its domain knowledge to quickly anticipate that an action choice is not appropriate. An autonomous character has no ability to make such judgments and, regardless of how appropriate it is, must blindly follow the predefined behavior rules that pertain to the current situation.
When there are many rules it is quite likely their applicability will overlap and they could give conflicting suggestions on which action to choose. In such cases some conflict resolution strategy must be employed.
It is often easier to write a controller if we can maintain some simple internal state information for the character. One popular way to do this is with HFSM that we discuss in the next section.
Hierarchical Finite-state Machines (HFSM)
Finite-state machines (FSMs) consist of a set of states (including an initial state), a set of inputs, a set of outputs, and a state transition function. The state transition function takes the input and the current state and returns a single new state and a set of outputs. Since there is only one possible new state, FSMs are used to encode deterministic behavior. It is commonplace, and convenient, to represent FSMs with state transition diagrams. A state transition diagram uses circles to represent the states and arrows to represent the transitions between states. Figure 2 depicts an FSM that keeps track of which compass direction a character is heading each time it turns "left".
As the name implies, an HFSM is simply a hierarchy of FSMs. That is, each node of an HFSM may itself be an HFSM. Just like functions and procedures in a regular programming language, this provides a convenient way to make the design of an FSM more modular. For example, if a character is at coordinates (x,y), Figure 3 depicts an HFSM that uses the FSM in Figure 2 as a sub-module to calculate the new cell after turning "left", or moving one cell ahead.
HFSMs are powerful tools for developing sophisticated behavior and it is easy to develop graphical user interfaces to assist in building them. This has made them a popular choice for animators and game developers alike.
HFSMs maintain much of the simplicity of sets of reactive-behavior rules but, by adding a notion of internal state, make it easier to develop more sophisticated behaviors. Unfortunately, they also have some of the same drawbacks. In particular, actions are chosen deterministically and there is no explicit separation of domain knowledge from control information. This can lead to a solution which is messy, hard to understand and all but impossible to maintain. Just like reactive-behavior rules, there can also be a large amount of work involved if we want to obtain even slightly different behavior from an HFSM.
Goal-Directed Behavior
The first step in describing goal-directed behavior is to come up with a way to define a cognitive character's goals. The situation calculus provides a simple and intuitive theoretical framework to explain how this can be done. In particular, a character's goals can be expressed in terms of the desired value of various relevant fluents. A goal can therefore be expressed as a defined fluent, i.e., a fluent defined in terms of other fluents. For example, suppose we have two characters, call them Dognap and Jack, such that Dognap is armed with a gun, and wants to kill Jack. Then, we can state that Dognap's goal is to kill Jack: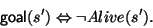 
Clearly, Dognap will have achieved this goal in any situation s' for which is goal(s') true. We recall that any situation is either the initial situation s0, or of the form:
Therefore, if goal(s0) is not true, then Dognap must search for a sequence of n actions, a0,...,an-1 such that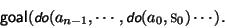 
is true.
Situation Tree
To explain how characters can automatically search for sequences of actions that meet their goals, we will introduce the idea of a situation tree. In particular, we can think of the actions and effects as describing a tree of possible future situations. The root of the tree is the initial situation s0, each branch of the tree is an action, and each node is a situation. Figure 4 shows an example of a tree with n actions, a0,a1...,an-1.
The value of the fluents at each node (situation) is determined by the effect axioms. Figure 5 shows a simple concrete example using the Dognap and Jack example, and the corresponding effect axioms, that we described earlier.
Figure 5 A concrete example of a situation tree. A goal situation is a situation in which the fluent is true. For example, in Figure 5 we can see that if the goal is still to kill Jack then the situation
is a goal situation. We can see that in this example there are many goal situations, for example
is another goal situation. In general, however, there is no guarantee that a goal situation exists at all. If a goal situation does exist, then any action sequence that leads to one of the goal situations is called a plan.
Figure 6 shows a simple abstract situation tree with just three actions, and three goal situations. We will use this figure to illustrate how a character can search the tree to automatically find a plan (a path) that leads from the initial situation (the root) to a goal situation. Depending on how we choose to search the tree we will find different plans (paths). In particular, we can see some common search strategies being applied. We can see that a bounded depth-first search strategy finds the plan [a0,a2,a0], whereas a breadth first search finds [a1,a2].
A breadth-first search tries exhaustively searching each layer of the tree before proceeding to the next layer. That is, it considers all plans of length 0, then all plans of length 1, etc. Thus, a breadth-first search is guaranteed to find a plan if there is one. Moreover it will find the shortest such plan. Unfortunately, a breadth-first search requires an exponential amount of memory as the character has to remember all the previous searches.
A depth-first search doesn't require an exponential amount of memory, as there is no need to explicitly store large portions of the tree. That is, a depth-first search only needs to remember one branch of the tree at a time. It keeps looking down this one branch until it gets to a goal, or it reaches a leaf node. If it reaches a leaf-node, it backs up to the previous node and searches another branch. If there are no more branches, it backs up one step further and proceeds recursively until it has searched the entire tree. Unfortunately, even if there is a goal in the tree, depth-first search is not guaranteed to find it. In particular, it is quite likely that the tree will have branches that are infinite. That is, the character can just keep doing some sequence of actions over and over again, but it never leads to a goal. A depth-first search can get sidetracked by searching down one of these fruitless infinite branches. Because it never reaches a goal, or a leaf node, the algorithm never terminates. Another drawback of a depth-first search is that even if it does find a plan, this plan is not guaranteed to be the shortest possible plan. Depending on the application, this may or may not be important.
A bounded depth-first search attempts to resolve some of the limitations of a depth-first search by putting a bound on how deeply in the tree the search can proceed. Now the search backs up if it finds a leaf node, or if the maximum search depth is exceeded. It is even possible to iteratively search with a deeper and deeper bound. To avoid redoing the work of the previous search, the results of the last search can be stored so that we don't have to begin from scratch each time the depth bound is increased. Unfortunately, we are now back to remembering large portions of the tree and, just like a breadth-first search, this requires an exponential amount of memory.
In the worst case, the situation tree does not contain any goal situations. If this is the case, then any exhaustive search algorithm will take an exponential amount of time to respond that there is no plan available to achieve the goal. This is one of the major limitations of planning and is something we will look at in more detail in the next section. In the meantime, we mention that looking for different search algorithms is an important topic in AI research and the interested reader should consult the further reading section. One of the most interesting new developments is the use of stochastic search algorithms.
It should also now be apparent how choosing actions nondeterministically entails searching for appropriate action sequences in a search space that potentially grows exponentially. This corresponds to the usual computer science notion of computational complexity. Another interesting point to note is that CPU processing power is also growing exponentially. Therefore, according to Moore's law, our computer characters can be expected to be able to search one layer deeper in the situation tree every eighteen months or so.
The Middle Ground
As we explained, for predefined behaviors the character doesn't have to do any searching for actions that achieve its goals. It simply follows the instructions it was given and ends up at a goal situation. In effect, for a given set of inputs, the path through the tree of possible situations has been determined in advance. If the predefined behaviors were defined properly, then the path that they specify through the tree will lead to a goal situation.
In this section, the question we want to ask is whether there is some middle ground between asking the character to do all the work at run-time and asking the programmer to all the work at compile time. In particular, consider that on the one hand we have predefined behavior which corresponds to a single path through the situation tree, and on the other hand we have goal-directed behavior which corresponds to searching the whole tree. Clearly, the middle ground has to be searching some subset of the tree.
Note that this "middle ground" is still technically goal-directed behavior, but we now have control over how much nondeterminism is allowed in the behavior specification. Only in the limiting case, when we have removed all the nondeterminism, does the behavior reduce to deterministic predefined behavior.
Precondition Axioms
Although we might not have realized it, we have already seen one way to exclude parts of the situation tree from the search space. In particular, precondition axioms prune off whole chunks of the tree by stating that not all actions are possible in all situations. Figure 7 shows an example of an abstract tree in which it is not possible to do an action a2 because an action a1 changed something which made it impossible.
While preconditions are important for cordoning off parts of the situation tree, they are a clumsy way to try and coerce a character to search a particular portion of the tree. In particular, we need a way to give a character general purpose heuristics to help it find a goal faster. For example, we might want to give the character a heuristic that will cause it look at certain groups of actions first, but we do not want to absolutely exclude the other actions.
The hard part of exploiting the middle ground between predefined and goal-directed behavior is to think up a useful way to specify subsets of the tree. In the next section, we will introduce a convenient way to specify arbitrary subsets of the situation tree to search.
Complex Actions
We would like to provide a character with a "sketch plan" and have it responsible for filling in the remaining missing details. In this way, we salvage some of the convenience of the planning approach while regaining control over the complexity of the planning tasks we assign the character. We will show how we can use the idea of complex actions to write sketch plans.
The actions we discussed previously, defined by precondition and effect axioms, are referred to as primitive actions. (The term "primitive action" is only meant to indicate an action is an atomic unit, and not a compound action. Unfortunately, the term can be misleading when the action actually refers to some sophisticated behavior, but we will stick with the term as it is widely used in the available literature). Complex actions are abbreviations for terms in the situation calculus; they are built up from a set of recursively defined operators. Any primitive action is also a complex action. Other complex actions are composed using various operators and control structures, some of which are deliberately chosen to resemble a regular programming language. When we give a character a complex action a, there is a special macro Do that expands a out into terms in the situation calculus. Since complex actions expand out into regular situation calculus expressions, they inherit the solution to the frame problem for primitive actions.
Complex actions are defined by the macro Do(a,s,s'), such that is a state that results from doing the complex action a in state s. The complete list of operators for the (recursive) definition of Do are given below. Together, the operators define an instruction language we can use to issue direction to characters. The mathematical definitions can be difficult to follow, and the reader is encouraged to consult the book [Funge99], in which we explain the basic ideas more clearly using numerous examples of complex actions (note there are two freely available implementations of complex actions that can be studied for a more practical insight into how the macro expansion works--see www.cs.toronto.edu/~funge/book).
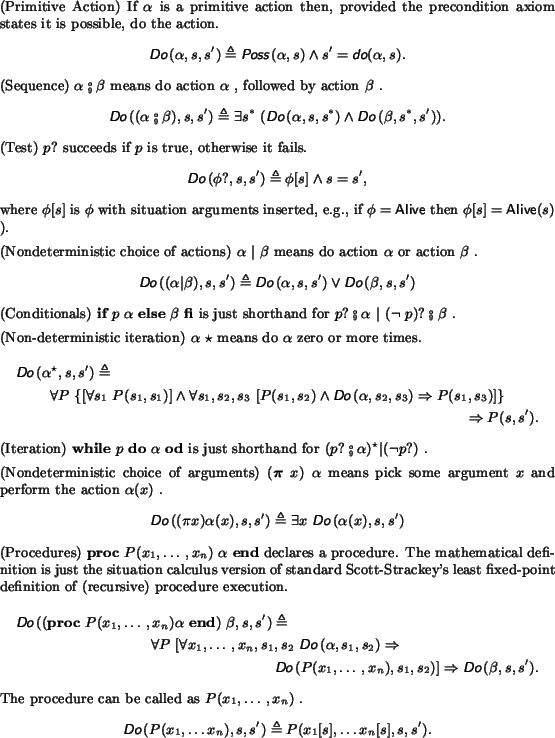
The macro expansion Do(a,s,s') specifies a relation between two situations s and s', such that is a situation that results from doing the complex action a in situation s. In general, there is not a unique s', so if we have some initial situation s0, a complex action "program", and a bunch of precondition and effect axioms, then Do(program, s0, s') specifies a subset of the situation tree. Figure 8 shows a quick example of how a complex action can be used to limit the search space to some arbitrary subset of the situation tree. The other thing we can see from the figure is that the mathematical syntax can be rather cryptic. Therefore, in the appendix, we introduce some alternative syntax for defining complex actions that is more intuitive and easy to read.
On its own, just specifying subsets of the situation tree is not particularly useful. Therefore, we would normally explicitly mention the goal within the complex action. We shall see many examples of this in what follows. For now, suppose the complex action "program" is such a complex action. If we can find any
such that Do(program, s0, s'), then the plan of length n, represented by the actions a0,...,an-1. , is the behavior that the character believes will result in it obtaining its goals. Finding such an s' is just a matter of searching the (pruned) situation tree for a suitable goal situation. Since we still end up searching, research in planning algorithms is just as relevant to this section as to the straight goal-directed specification section.
Implementation
Note that we defined the notion of a situation tree to help us visualize some important ideas. We do not mean to suggest that in any corresponding implementation that there need be (although, of course, there may be) any data structure that explicitly represents this tree. In particular, if we explicitly represent the tree, then we need a potentially exponential amount of memory. Therefore, it makes more sense to simply build portions of the tree on demand, and delete them when they are no longer required. In theorem provers and logic programming languages (e.g., Prolog), this is exactly what happens continually behind the scenes.
Logic programming languages also make it straightforward to under-specify the domain knowledge. For example, it is perfectly acceptable to specify an initial state that contains a disjunction, e.g. OnTable(cup,s0) v OnFloor(cup,s0). Later on, we can include information that precludes a previously possible disjunct, and the character will still make valid inferences without us having to go back and alter any of the previous information. If we do not need such a sophisticated notion of elaboration tolerance, then it might be simpler to build a situation tree explicitly. Moreover, if the tree is not too deep, or if it is heavily pruned, it needn't be excessively large and thus can be fast to search. Whether such a shallow, or sparse, tree is useful or not will depend on the particular application, but in computer games and animation there are countless examples where a character with even a moderate ability to plan ahead can be extremely useful.
A Simple Tutorial Example: Maze Solving
We already looked at some predefined behavior for solving a maze. Let's take a look at a goal-directed approach to the problem. Of course, since there are well-known predefined behaviors for maze solving, we would not suggest using a goal-directed approach in a real application. Therefore, this section is simply meant as a tutorial example to show how some of the different pieces fit together.
Domain Knowledge
Let us suppose we have a maze defined by a predicate Free(c), that holds when, and only when, the grid cell c is "free". That is, it is within range and is not occupied by an obstacle.
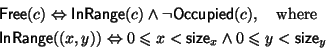
Occupied(c), sizex, and sizey each depend upon the maze in question. In addition, there are two maze dependent constants start and exit that specify the entry and exit points of a maze. Figure 9 shows a simple maze and the corresponding definition.
We also need to define some functions that describe a path within the maze. We say that the adjacent cell "North" of a given cell is the one directly above it, similarly for "South", "East", and "West".
There are two fluents; position denotes which cell contains the character in the current situation, and visited denotes the cells the character has previously visited.
The single action in this example is a move action that takes one of four compass directions as a parameter. It is possible to move in some direction d, provided the cell to which we are moving is free and has not been visited before.
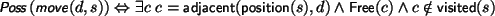
Figure 10 shows the possible directions a character can move when in two different situations.
A fluent is completely specified by its initial value and its successor-state axiom. For example, the initial position is given as the start point of the maze and the effect of moving to a new cell is to update the position accordingly.
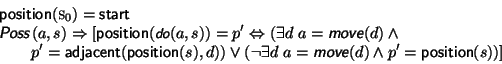
So for example, in Figure 9, if the character has previously been to the locations marked with the filled dots, and in situation the character moves north to the unfilled dot, then we have that position(s) = (2,0) and that position(do(move(north),s)=(2,1).
The list of cells visited so far is given by the defined fluent . It is defined recursively on the situation to be the list of all the positions in previous situations (we use standard Prolog list notation).
For example, in Figure 9, when
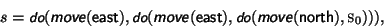
we have that (s) = (2,1), and that (s) = [(2,0,(1,0),(0,0)].
Character Instruction
We have now completed telling the character everything it needs to know about the concept of a maze. Now we need to move on and use complex actions to tell it about its goal and any heuristics that might help it achieve those goals. As a first pass, let's not give it any heuristics, but simply provide a goal-directed specification of maze-solving behavior. Using complex actions we can express this behavior elegantly as follows:
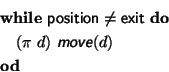
Just like a regular "while" loop, the above program expands out into a sequence of actions. Unlike a regular "while" loop, it expands out, not into one particular sequence of actions, but into all possible sequences of actions. The precondition axioms that we previously stated, and the exit condition of the loop, define a possible sequence of actions. Therefore, any free path through the maze, which does not backtrack and ends at the exit position, meets the behavior specification.
Note that the use of regular programming constructs may initially cause confusion to the reader of the above code. Most of the work is being done by the nondeterministic choice of arguments operator "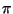
". The example makes it clear that by "nondeterministic" we do not mean that anything random is happening; we simply mean that we can specify a large number of possibilities all at once. In particular, the (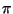d) construct should be read as "pick the correct direction d". For the mathematically inclined, perusing the definitions may serve to alleviate any sense of bewilderment. To make things even clearer we shall, however, consider the expansion of the complex actions in terms of their definitions. The expansion is based on the simple maze described previously in Figure 9.
In the initial situation we have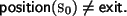 
. Thus the guard of the "while" loop holds and we can try to expand
Expanding this out into the full definition gives
However, from the action preconditions for and the definition of the maze we can see that:
This leaves us with s = do(move(north), s0) V s = do(move(east), s0).That is, there are two possible resulting situations. That is why we refer to this style of program as nondeterministic.
In contrast, in situation s = do(move(north),s0) there is only one possible resulting situation. We have Do((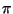d) move(d),s,s') that expands out into s'=do(move(north),s).
If we expand out the macro
from start to finish, we get
So, as depicted in Figure 11, our "program" does indeed specify all paths through the maze.
Although we disallow backtracking in the final path through the maze, the character may use backtracking when it is reasoning about valid paths. In most of the mazes we tried, the character can reason using a depth-first search to find a path through a given maze quickly. For example, Figure 12 shows a path through a reasonably complicated maze that was found in a few seconds.
To speed things up, we can start to reduce some of the nondeterminism by giving the character some heuristic knowledge. For example, we can use complex actions to specify a "best-first" search strategy. In this approach, we will not leave it up to the character to decide how to search the possible paths, but constrain it to first investigate paths that head toward the exit. This requires extra lines of code, but could result in faster execution.
For example, suppose we add an action goodMove(d), such that it is possible to move in a direction d if it is possible to "move" to the cell in that direction and the cell is closer to the goal than we are now.
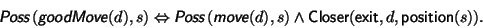
Now we can rewrite our high-level controller as one that prefers to move toward the exit position whenever possible.>
At the extreme, there is nothing to prevent us from coding in a simple deterministic strategy such as the "left-hand" rule. For example, if we introduce a defined fluent dir that keeps track of the direction the character is traveling, and a function ccw that returns the compass direction counterclockwise to its argument, then the following complex action implements the left-hand rule.
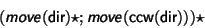
The important point is that using complex actions does not rule out any of the algorithms one might consider when writing the same program in a regular programming language. Rather, it opens up new possibilities for high-level specifications of behavior at a cognitive level of abstraction.
Discussion
Complex actions provide a convenient tool for giving a character "advice" in the form of heuristic rules that will help it solve problems faster. In general, the search space will still be exponential, but reducing the search space can make the difference between a character that can plan 5 steps ahead, say, and one that can plan 15 steps ahead. That is, we can get characters that appear a lot more intelligent.
The possibility also exists for incremental refinement of a specification, perhaps, from a high-level specification to the point where it more closely resembles a controller written using a conventional imperative programming language. That is, we can quickly create a working prototype by relying heavily on goal-directed specification. If this prototype is too slow, we can use complex actions to remove more and more of the nondeterminism. If required, we can even do this to the point where the behavior is completely predefined.
To sum up, if we can think of, or look up, a simple predefined way to produce the behavior we are interested in, then it makes a lot of sense to use it. This is especially so if we don't think the behavior will need to be modified very often, or at least if the anticipated modifications are minor ones. It is not surprising, therefore, that a lot of simple reactive behavior is implemented using simple reactive behavior rules. For simple reactive behavior, like collision avoidance, it is not hard to think of a small set of reactive behavior rules that will do the job. Moreover, once we have this set of rules working, it is unlikely that we will need to modify it.
We have tried to make it clear that one type of behavior can be implemented using a variety of techniques. We have, therefore, chosen not to classify behavior according to what the character is trying to achieve, but rather on the basis of the technique used to implement it. The reader should note however that some others do try to insist that behavior in the real world is of a certain type, and its virtual world counterpart must therefore be implemented in a particular way. Unfortunately, this leads to lots of confusion and disagreement among different research camps. In particular, there are those who advocate using predefined behavior rules for implementing every kind of behavior, no matter how complex. In the sense that, given enough time and energy it can be done, they are correct. However, they are somewhat like the traditional animator who scoffs at the use of physical simulators to generate realistic-looking motion. That is, to the traditional animator a physical simulator is an anathema. She has an implicit physical model in her head and can use this to make realistic motion that looks just as good (if not better), and may only require the computer to do some simple "inbetweening". Compared to the motion that needs a physical simulator to execute, the key-framed approach is lightning fast. If we could all have the skill of a professional animator there would not be so much call for physical simulators. Unfortunately, most of us do not have the skill to draw physically-correct looking motion and are happy to receive all the help we can get from the latest technology. Even artists who can create the motion themselves might prefer to expend their energies elsewhere in the creative process.
In the same vein, many of us don't have any idea of how to come up with a simple set of stimulus-response rules that implement some complex behavior. Perhaps, we could eventually come up with something, but if we have something else we'd rather do with our time it makes sense to get the characters themselves to do some of the work for us. If we can tell them what we want them to achieve, and how their world changes, then perhaps they can figure it out for themselves.
We should also point out that there are those who advocate a cognitive modeling approach for every kind of behavior, even simple reactive ones. This view also seems too extreme as, to coin a phrase, there is no point "using a sledgehammer to crack a nut". If we have a simple reactive behavior to implement, then it makes sense to look for a simple set of predefined rules. Also, if lightning-fast performance is an absolute must, then we might be forced to use a predefined approach, no matter how tough it is to find the right set of rules.
Of course, there is a big gray area in which there is no clear answer as to whether we should just stick with predefined behavior rules or not. In such cases, the choice of how to proceed can depend on personal preference and the available tools and expertise. Obviously, this article is primarily aimed for those who decide to go the cognitive modeling route.
Notes
For some basic information on FSMs see [HU79]. For more in-depth information on predefined behavior techniques, consult [Maes90,BBZ91,Tu99]. There are even some commercial character development packages that use HFSMs to define character behavior. See [Nayfeh93] for a fascinating discussion on maze-solving techniques. Many of the classic papers on planning can be found in [AHT90]. See [SK96] for some work on the use of stochastic techniques for planning. Prolog is the best known nondeterministic programming language and there are numerous references, for example see [Bratko90].
The complex action macro expansion is closely related to work done in proving properties of computer programs [GM96]. Our definitions are taken from those given in [LRLLS97]. A more up-to-date version, that includes support for concurrency, appears in [LLR99]. See [Stoy77] for the Scott-Strackey least fixed-point definition of (recursive) procedure execution.
References
[AHT90] J. Allen, J. Hendler, and A. Tate, editors. Readings in Planning. Morgan Kaufmann, San Mateo, CA, 1990.
[BBZ91] N.I. Badler, B.A. Barsky, and D.Zeltzer, editors. Making Them Move: Mechanics, Control, and Animation of Articulated Figures. Morgan Kaufmann, San Mateo, 1991.
[Bratko90] I. Bratko. PROLOG Programming for Artificial Intelligence. Addison Wesley, Reading, MA, 1990.
[Funge99] J. Funge. AI for Games and Animation: A Cognitive Modeling Approach. A. K. Peters. Natick, MA, 1999.
[GM96] J. A. Goguen and G. Malcolm. Algebraic Semantics of Imperative Programs. MIT Press, Cambridge, MA, 1995.
[HU79] J. E. Hopcroft and J. D. Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, Reading, MA, 1979.
[LLR99] Y. Lespérance, H. J. Levesque, and R. Reiter. A Situation Calculus Approach to Modeling and Programming Agents. In A. Rao and M. Wooldridge, editors, Foundations and Theories of Rational Agency. Kluwer, New York, 1999. (See also: www.cs.toronto.edu/cogrobo)
[LRLLS97] H. Levesque, R. Reiter, Y. Lespérance, F. Lin, and R. Scherl. Golog: A Logic Programming Language for Dynamic Domains. Journal of Logic Programming, 31:59-84, 1997.
[Maes90] P. Maes (editor). Designing Autonomous Agents: Theory and Practice from Biology to Engineering and Back. MIT Press, Boston, 1990.
[Nayfeh93] B. A. Nayfeh. "Using a Cellular Automata to Solve Mazes." Dr. Dobb's Journal, February 1993.
[SK96] B. Selman and H. Kautz. "Knowledge compilation and theory approximation." Journal of the ACM, 43(2):193-224, 1996.
[Stoy77] J. E. Stoy. Denotational Semantics: The Scott-Strachey Approach to Programming Language Theory. MIT Press, Cambridge, MA, 1977.
[Tu99] X. Tu. Artificial Animals for Computer Animation: Biomechanics, Locomotion, Perception, and Behavior. ACM Distinguished Ph.D Dissertation Series, Springer-Verlag, 1999.
John Funge recently joined a research group at Sony Computer Entertainment America (SCEA) that investigates software issues related to the PlayStation. Previously John was a member of Intel's microcomputer research lab. He received a B.Sc. in Mathematics from King's College London in 1990, an M.Sc. in Computer Science from Oxford University in 1991, and a Ph.D. in Computer Science from the University of Toronto in 1997. For his Ph.D. John successfully developed a new approach to high-level control of characters in games and animation. John is the author of numerous technical papers and his new book "AI for Games and Animation: A Cognitive Modeling Approach" is one of the first to take a serious look at AI techniques in the context of computer games and animation. His current research interests include computer animation, computer games, smart networked devices, interval arithmetic and knowledge representation.
Read more about:
FeaturesYou May Also Like
