Terrain rendering is a popular area of research in modern games. From Microsoft’s Flight Simulator series to Bungie’s Halo, games that take place in the outdoors have to be able to render large areas of terrain in an efficient manner.

The most prominent method for achieving this on modern hardware is a method called level of detail. The idea behind level of detail is simple; do less processing on pieces of terrain that are very far away from the user’s viewpoint so that more processing can be focused on areas that the user can clearly see. This article will focus on a branch of the level of detail concept known as discrete level of detail (DLOD).

I will be presenting a new technique for generating index buffers that can be used when implementing discrete level of detail in terrain rendering. This algorithm addresses specifically the issue of index buffer generation, but also has a few extra benefits as a byproduct of the technique. For comparison with current techniques, I will be referring to an article written by Greg Snook that addresses LOD using an approach called interlocking tiles (ILT). I will point out some of the drawbacks of ILT and how using binary triangle trees (BTT) can eliminate them. Greg’s article can be found in Game Programming Gems 2 [Snook01].

What we’re really trying to do with LOD is optimize the rendering pipeline by sending down fewer triangles for pieces of terrain that are far away from the camera. As the distance to the camera increases, the number of distant triangles being represented by a small number of pixels increases. We can save time in the rendering pipeline by reducing the number of distant triangles that are being rendered. Discrete level of detail is achieved by using different index buffers to represent different sets of triangles using the same patch of vertices. Each patch is a square section of vertices. The total size of the vertex patches must conform to equation 1.

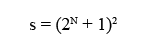
Equation 1: Where s is the total number of vertices in the patch

In this equation, n will be the deciding factor in how big your patches are, as well as how many levels of detail are possible with that patch. We’ll talk shortly about how n relates to the number of detail levels.

Figure 1 illustrates how a single patch of vertices can be used to represent different levels of detail. This figure is shown with the triangles laid out as they are in the ILT system.

Figure 1: The same vertices can be used to render different levels of detail

You can see here that these patches are 17x17, conforming to our previously stated equation (2n + 1)2, where n = 4. The patch on the left is using an index buffer that specifies only 8 triangles, while the patch on the right is using an index buffer specifying 32 triangles. This idea is the basis for DLOD in terrain rendering. As patches move farther away from the camera, index buffers with a lower triangle count can be used to represent the patch.

We can notice one problem right away, which is that when patches of different detail levels are placed next to each other, T-junctions form on the borders creating nasty cracks in the terrain. This problem is illustrated in figure 2.

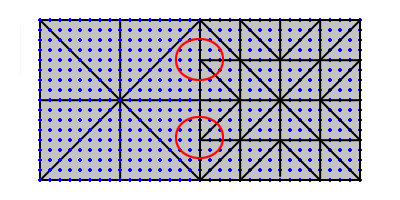
Figure 2: T-Junctions occur between patches of different detail levels

In the ILT system, the solution to this problem is to create linking pieces. Linking pieces take into account the neighboring patches’ LOD and use index buffers that were built specifically to link up to those levels. Figure 3 demonstrates this principle.

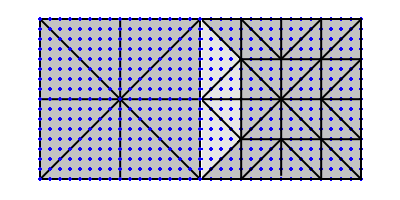
Figure 3: The lighter colored area shows the linking piece used to eliminate the T-Junctions

As you can see in Figure 3, the ugly T-Junctions are now gone and our terrain would be nice and smooth at this point. However, these linking pieces must be defined by hand for all four sides of the patch, and for each level of detail. In addition, 16 body pieces must be defined for each level of detail. Each of these body pieces makes room for different variations of linking pieces. Table 1 shows the number of buffers that have to be created for a patch with 4 levels of detail.

Table 1: Index buffers required for ILT

So, we see that it requires a total of 72 different index buffers to set up a terrain with four levels of detail. One of the major issues with ILT is that as the level of detail gets higher, the number of linking pieces for each side becomes greater, resulting in ever increasing memory usage. We’ll see how this is totally eliminated using BTT shortly.

Another problem with ILT is that there is currently no way to generate these index buffers. Each body and linking piece has to be defined by hand. The inflexibility with this approach was the leading factor in my decision to research and implement a new technique. If you’d like a more in depth coverage on ILT, please refer to [Snook01] in the references section at the end of this article. Let’s move on to the new technique and see how we can use binary triangle trees to generate our index buffers and get some huge improvements for free on the side.

The idea behind binary triangle trees is simple. A triangle can be recursively bisected into two sub triangles whose vertices are related to their parent’s in a consistent pattern. If we’re using a patch of vertices that is defined according to our patch requirements [(2n + 1)2], each vertex of the new triangles will evenly match up with a vertex in the patch. Figure 4 illustrates this principle with a simplified patch of only 5x5 vertices.

When using BTT, each level of detail is defined as the splitting of all triangles in a given patch one time. It is interesting to note here that this means the number of detail levels available for a single patch is not calculated in the same way as in ILT. Equation 2 shows how to calculate how many levels of detail are available for a given patch size when using ILT.

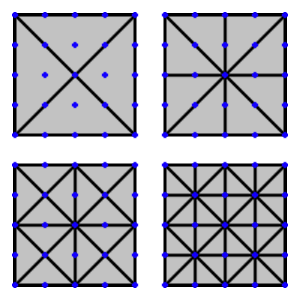
Figure 4: Recursively splitting triangles will eventually use up all of the vertices in a patch

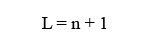
Equation 2: Where L is the levels of detail and n is the patch size exponent from Equation 1

For example, a 5x5 patch would be able to produce 3 levels of detail when using ILT. So, for each patch size increase, one extra level of detail will be attained. The following table shows the levels of detail possible with a given set of patch sizes when using ILT.

Table 2: Levels of detail possible for various patch sizes using ILT

The equation for calculating the number of detail levels for a given patch when using BTT is similar to Equation 2.

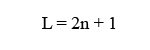
Equation 3: Where L is the levels of the detail and n is the patch size exponent from Equation 1

So we can see that by using BTT, the number of detail levels that can be achieved is almost a two fold increase over using ILT. Table 3 illustrates this.

Table 3: Levels of detail possible for various patch sizes using BTT

With the ability to have all these extra detail levels, you might think we’re going to be using way more index buffers and talking up tons more memory, right? Well, that actually isn’t the case at all. When using ILT, we had to create 16 body pieces for each level of detail, as well as all the linking pieces, in order to eliminate T-Junctions in the terrain. When using BTT, the concept of linking pieces is completely removed, and all we need are 15 index buffers. The linking information is built right into the patches, so extra linking piece buffers are not needed. In addition, only half of the detail levels need to link at all! Figure 5 illustrates this principle.

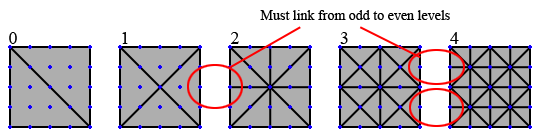
Figure 5: Half of the detail levels only require 1 buffer!

As you can see from the image, we only need to facilitate linking for odd detail levels. If you look at detail level two, you can see that it already seamlessly links to detail level three without us having to do any extra work! Two simple rules allow us to achieve this huge savings in memory. First, we make a simple rule that no neighboring patches can be more than 1 detail level away from each other. This isn’t really an issue in practice, because detail levels are assigned in a very linear fashion and are usually based on the distance from the camera. Second, patches will only link to detail levels that are higher than their own. Table 4 shows the index buffer usage for a 5x5 patch using BTT. Compare to Table 1.

Table 4: Index buffers required for BTT

If you look back at Table 1 you can see that ILT uses twice as many index buffers as BTT and produces one less level of detail. So not only are we using less memory, but we’re also getting more detail levels. Another interesting thing to note about the performance of these two techniques is that ILT may require up to 5 index buffers being sent to the graphics card for any given patch. That would be the body plus 4 linking pieces. BTT always requires only 1 index buffer to be sent for each patch, regardless of its detail level or what it is linking to.

We’ve seen how using BTT can be an improvement over ILT as far as performance and memory usage, now we’ll talk a look at what really makes this technique shine – algorithmic generation of index buffers.

There are two key objects in the BTT algorithm for generating index buffers. First, we need to specify a triangle object that can be recursively subdivided into two smaller triangles. Second, we need a tile class that will be made up of these triangle objects in order to handle the higher level concept of a patch. For simplicity, I’m not going to be including any source code in this article. There is a demo available with source code included so you can take a look for yourself and see how it works internally. We’ll just stick to theory here.

A 5x5 patch will be our example for the remainder of the article. First, we’ll look at the special case level of detail 0. This level doesn’t require any triangle objects and can be defined by hand as it is only 6 indices. Figure 6 shows this case.

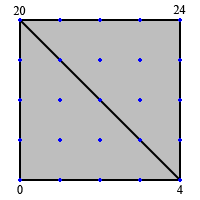
Figure 6: Level 0 is a special case that can be defined by hand

The index buffer here is just going to be six elements defining two unique triangles. Assuming a clockwise winding order, the indices would be { (0, 20, 4), (24, 4, 20) }. Note that we always start from the apex of the triangle when defining the index buffers. This level doesn’t have any linking cases so we’re done!

Level 1 is where we really start to get into using BTT and we’ll see here why they are so well suited for this task. Take a look at Figure 7.

Figure 7: Level 1 is made up of 4 triangles

Ok, so here is the main base patch. Basically what we’re looking at here is a patch with 4 triangles (It’s important to remember that in the construction of the patch, you will need to supply the starting vertices indices for each of the base triangles. The base indices are what will be used during the rest of the splitting operations). Each triangle is labeled with a cardinal direction. This is important because it will help us with understanding the linking portion later. At this point, we could continue to generate base detail levels by simply splitting each triangle. Figure 8 shows what base level 2 looks like.

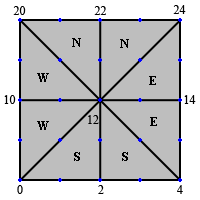
Figure 8: Base level 2 is generated by simply splitting all the triangles

This is what detail level two would look like. Note that each child triangle is tagged with its parent’s direction. However, just generating base detail levels isn’t quite enough. We know that detail level 1 needs extra buffers to handle linking, so how are we going to do that? Well, the tile is keeping track of 4 main triangles (N, S, E, W), and each triangle can be split independently. If, for instance, we wanted to generate a level 1 triangle that would link up to a level 2 triangle on the east, we just split the east triangle once. Figure 9 shows what this looks like.

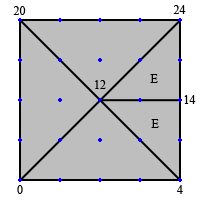
Figure 9: Level 1 with a split on the east triangle to link up to a level 2

So this would handle the case of linking up to a higher detail level on the east, but remember that we have a total of 14 combinations that might come up. Figure 10 shows the index buffers that need to be generated for every odd detail level.

Figure 10: The 14 index buffers needed for odd detail levels

Figure 10 shows all of the index buffers we will ever need to handle linking between detail levels. By examining the neighboring tiles, we can figure out which linking buffer to use based in which sides are bordered by higher detail levels. The final selected buffer is the only index buffer required to be sent to the card. Let’s talk a little bit about the details of splitting triangles.

It’s important to keep track of the triangle's original direction tag when splitting to produce its children. Each child needs to be either tagged with its parent’s direction, or tagged as “inner.” Inner triangles are those that don’t touch the tile border and do not need to be considered for further splitting. Figure 11 shows an example of inner triangles as a result of splitting.

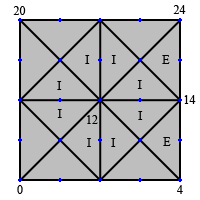
Figure 11: Inner triangles produced a result of splitting

You can see that the second generation of eastern triangles has been split to produce two inner triangles. These triangles do not touch the borders of other tiles so they do not need to be considered for further splitting. Figure 12 illustrates how inner triangles can be safely ignored when splitting to the next detail level.

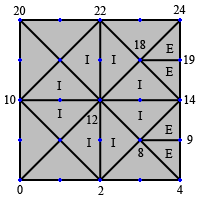
Figure 12: Inner triangles can be ignored in subsequent splitting operations

We can see that the third generation of eastern triangles can continue to be split as normal, and that the inner triangles are unaffected. This pattern will continue to be reproduced in the same way as we keep splitting to higher detail levels. In order to actually generate the index buffer for this tile, and all the other tiles we generate, we simply need to loop through each leaf triangles in the tree and add its three vertex indices to the final buffer.

In conclusion, I’ll recap on the pros and cons of using binary triangle trees for discrete level of detail in terrain rendering.

Pros:

Cons:

References:

[Snook01] Snook G., “Simplified terrain using interlocking tiles”, Game Programming Gems 2, Charles River Media, 2001