Building a Million-Particle System

Particle systems have long been recognized as an essential building block for detail-rich and lively visual environments. Current implementations can handle up to 10,000 particles in realtime simulations and are mostly limited by the transfer of particle data from the main processor to the graphics hardware (GPU) for rendering.

This article introduces a full GPU implementation of both the simulation and rendering of a dynamically-growing particle system. Such an implementation can render up to 1 million particles in real-time on recent hardware. It helps you to dramatically increase the level of detail and allows you to simulate much smaller particles. Thus it goes back again towards the original idea of a particle being a minimal geometry element.

The massively parallel simulation of particle physics on a GPU can be a flexible combination of a multitude of motion and position operations, e.g. gravity, local forces and collision with primitive geometry shapes or texture-based height fields. Additionally, a parallel sorting algorithm is introduced that can be used to perform a distance-based sorting of the particles for correct alpha-blended rendering.

Why Particle Systems?

Reality is full of motion, full of chaos and full of fuzzy objects. Physically correct particle
systems (PS) are designed to add these essential properties to the virtual world. Over the last decades they have been established as a valuable technique for a variety of volumetric effects, both in real-time applications and in pre-rendered visual effects of motion pictures and commercials.

Particle systems have a long history in video games and computer graphics. Very early video games in the 1960s already used 2D pixel clouds to simulate explosions. The first publication about the use of dynamic PS in computer graphics was written after the completion of the visual effects for the motion picture Star Trek II at Lucasfilm (cf. [Reeves1983]). Reeves describes basic motion operations and basic data representing a particle –- neither have been altered much since. An implementation on parallel processors of a super computer has been done by [Sims1990]. He and [McAllister2000] also describe many of the velocity and position operations of the motion simulation that are used below. The latest description of CPU-based PS for use in video games has been done by [Burg2000].

Real-time PS are often limited by the fill rate or the CPU to graphics hardware (GPU) communication. The fill rate, the number of pixels the GPU can draw for each frame, is often a limiting factor when there is a high overdraw, i.e. single particles are relatively large and a lot of them overlap each other. Since the realism of a particle system simulation increases when smaller particles are used, the fill rate limitation loses importance. The second limitation, the transfer bandwidth of particle data from the simulation on the CPU to the rendering on the GPU, now dominates the system. Sharing the graphics bus with many other rendering tasks allows CPU-based PS to achieve only up to 10,000 particles per frame in typical game applications. Therefore it is desirable to minimize the amount of communication of particle data. This can be achieved by integrating both parts, simulation and rendering, of this visualization problem on the GPU.

To simulate particles on a GPU you can use stateless or state-preserving PS. Stateless PS require a particle's data to be computed from its birth to its death by a closed form function which is defined by a set of start values and the current time. State-preserving PS allow using numerical, iterative integration methods to compute the particle data from previous values and a changing environmental description (e.g. moving collider objects). Both simulation methods have their areas of applications and are to be chosen based on the requirements of the desired effect.

Stateless PS have been introduced on the first generation of programmable PC GPUs (cf. [NVIDIA2001]) and are described in "Stateless particle systems". The state-preserving simulation introduced here is described in "Particle simulation on graphics hardware". Besides the particle system itself additional innovations are the usage of simulated pixel data as geometry input (cf. "Transfer texture data to vertex data") and the sorting of this data with a parallel sorting algorithm (cf. "Sort for alpha blending"). These innovations are applicable to other algorithms as well.

Several other forms of physical simulation have recently been developed for modern GPUs. [Harris2003] has used GPUs to perform fluid simulations and cellular automata with similar texture-based iterative computation. [Green2003] describes a cloth simulation using simple grid-aligned particle physics, but does not discuss generic particle systems' problems, like allocation, rendering and sorting. The photon mapping algorithm described by [Purcell2003] uses a sorting algorithm similar to the odd-even merge sort in "Sort for alpha blending". However their algorithm does not show the necessary properties to exploit the high frame-to-frame coherence of the particle system simulation.

Prior work

This section describes two basis techniques for particle systems: stateless particle simulation and general-purpose computation on graphics hardware related to this work.

Stateless Particle Systems

Some PS have been implemented with vertex shaders (also called vertex programs) on programmable GPUs [NVIDIA2001]. These PS are however stateless, i.e. they do not store the current positions and other attributes of the particles. To determine a particle's position you need to find a closed form function for computing the current position only from initial values and the current time. As a consequence such PS can hardly react to a dynamic environment.

Particles that are not meant to collide with the environment and that are only influenced by global gravity acceleration can be simulated quite easily with a simple function. But simple collisions or forces with local influence however lead to rather complex functions.

Particle attributes besides velocity and position, e.g. the particle's orientation, size and texture coordinates, have generally much simpler computation rules. It is often sufficient to calculate them from a start value and a constant factor of change over time, which makes them ideal for a stateless simulation. This holds true even if the position is determined with the statepreserving simulation as described below (cf. "Particle simulation on graphics hardware").

The strengths of the stateless PS make it ideal for simulating small and simple effects without influence from the local environment. In action video games these might be a weapon impact splash or the sparks of a collision. Larger effects that require interaction with the environment are less suitable for the technique.

General-Purpose Computation on Graphics Hardware

With the broad availability of programmable graphics hardware, much research has been done to explore non-graphical uses of graphics hardware. Besides the work mentioned in "Introduction", a good overview about recent research can be found at [GPGPU2003].

A common abstraction of the programming model available in graphics hardware is called “stream programming” (cf. [Buck2003]): An input data stream is transformed by an autonomous processing kernel that then produces an output data stream. The processing kernel itself has read-only access to the input stream and global data, but it can only write one output data record.

In graphics hardware terms the input data stream can be represented by a texture, the output data stream by a render target. Output data is often re-used as input in a further processing step. In that case the data streams are textures as well as render targets. The processing kernel is represented by a pixel shader (also called fragment program). By drawing a full-screen rectangle, the graphics hardware is instructed to call the pixel shader once for each output data record, reading from the input stream in the pixel shader.

______________________________________________________

Particle Simulation on Graphics Hardware

The following sections describe the algorithm of a state-preserving particle system on a GPU in detail. After a brief overview, the used graphics hardware features, the storage and then the processing of particles is described.

Algorithm Overview

The state-preserving particle system stores the velocities and positions of all particles in textures. These textures are also render targets. In one rendering pass the texture with particle velocities is updated according to the stream processing model (cf. "General-purpose computation on graphics hardware"). The update performs one time step of an iterative integration which applies acceleration forces and collision reactions. Another rendering pass updates the position textures in a similar way, using the just computed velocities for the position integration. Depending on the integration method it is possible to skip the velocity update pass, and directly integrate the position from accelerations.

Optionally, the particle positions can be sorted depending on the viewer distance to avoid rendering artifacts later on. The sorting performs several additional rendering passes on textures that contain the particle distance and a reference to the particle itself.

Then the particle positions are transferred from the position texture to a vertex buffer. Finally this geometry data is rendered to the screen in a traditional way – as point sprites or primitive triangles or quads.

Hardware Requirements

The simulation on the GPU requires functionality that has only recently become available in PC graphics hardware. One key functionality is a floating point programmable pixel pipeline. The other one is a mechanism for communicating pixel data to the vertex pipeline. The latter is already common on video game consoles with unified memory access, whereas it is quite new in PC graphics hardware. "Transfer texture data to vertex data" discusses two approaches to this problem.

The algorithm's application to video game console hardware is only limited, though. The Microsoft Xbox offers 8-bit precision in the pixel pipeline. It is only capable of performing a low precision simulation, which limits the maximum extents of the particle system. Compared to PC hardware, the Sony PlayStation 2 is architecturally quite different and it does not offer a programmable pixel pipeline. Its programmable geometry unit is however capable of running the stateless particle simulation (cf. "Stateless particle systems") quite efficiently.

As details about the upcoming generation of video game consoles are not publicly available at this time, one can only speculate about their capabilities. Considering the trend towards increased parallel computation, it can be assumed that a parallel physical particle simulation is at least conceptually suitable for these devices.

Particle Data Storage

The most important attributes of a particle are its position and velocity. The positions of all active particles are stored in a floating point texture with three color components that will be treated as x, y and z coordinates. Each texture is conceptually treated as a one-dimensional array, texture coordinates representing the array index. The actual textures however need to be two-dimensional due to the size restrictions of current hardware. The texture itself is also a render target, so it can be updated with the computed positions. In the stream processing model (covered in the section "General-purpose computation on graphics hardware"), it represents either the input or the output data stream. As a texture cannot be used as input and output at the same time, we use a pair of these textures and a double buffering technique to compute new data from the previous values (see Figure 1).

A pair of velocity textures can be created in the same way as the position textures. Due to their reduced precision requirements it is usually sufficient to store the velocity coordinates in 16-bit floating point format. Depending on the integration algorithm there is no need to store the velocity explicitly (cf. "Update positions"). If the velocity is not stored in textures, you need a third position texture, which basically forms a triple buffer.

If other particle attributes (like orientation, size, color, and opacity) were to be simulated with the iterative integration method, they would need texture double buffers as well. However, since these attributes typically follow simple computation rules or are even static, we can take a simpler approach. An algorithm similar to the stateless particle system (cf. "Stateless particle systems") can be used to compute these values only from the relative age of the particle and a function description, e.g. initial and differential values or a set of keyframes. To be able to evaluate this function, we need to store two static values for each particle: its time of birth and a reference to a set of attribute parameters for its particle type. They are stored in a further texture, but the double buffer approach is not necessary.

We assume that the particles can be grouped by a particle type in order to minimize the amount of static attribute parameters that need to be uploaded during the final rendering of the particles. This particle type can either be directly coupled in a one-to-one relationship to the particle emitter or a group of emitters emits all particles of the same type.

The mass of a particle needs to be known to calculate accelerations from forces. Possible approaches are: treating all particles as having equal mass, uploading a mass value or function as particle type parameters, or storing the mass of each particle in the static data texture described above.

To sum up: a single particle consists of data values spread between several textures, but placed at equal texture coordinates in all those textures. According to demand particle type parameters also allow the computation of further particle values.

Simulation and Rendering Algorithm

The algorithm consists of six basic steps:

1. Process Birth and Death

The particles in a system can either exist permanently or only for a limited time. A static number of permanently existing particles represents the simplest case for the simulation, as it only requires uploading all initial particle data to the particle attributes textures once. As this case is rather rare, we assume a varying number of short-living particles for the rest of the discussion. The particle system must then process the birth of a new particle, i.e. its allocation, and the death of a particle, its deallocation.

The birth of a particle requires associating new data with an available index in the attribute textures. Since allocation problems are serial by nature, this cannot be done efficiently with a data-parallel algorithm on the GPU. Therefore an available index is determined on the CPU via traditional fast allocation schemes. The simplest allocation method uses a stack filled with all available indices. A more complex allocator uses a heap data structure that is optimized to always return the smallest available index. Its advantage is that if a particle system has a highly varying number of particles, the particles remain packed in the first portion of the system. The following simulation and rendering steps only need to update that portion of data, then. After the index has been determined, the new particle's data is rendered as single pixel into the attribute textures. This initial particle data is determined on the CPU and can use complex algorithms, e.g. various probability distributions for initial starting positions and directions etc. (cf. [McAllister2000])

A particle's death is processed independently on the CPU and GPU. The CPU registers the death of a particle and adds the freed index to the allocator. The GPU does an extra pass over the particle data: The death of a particle is determined by the time of birth and the computed age. The dead particle's position is simply moved to invisible areas, e.g. infinity. As particles at the end of their lifetime usually fade out or fall out of visible areas anyway, the extra pass rarely really needs to be done. It is basically a clean-up step to increase rendering efficiency.

2. Update Velocities

The first part of the simulation updates the particles' velocity. The actual program code for the velocity simulation is a pixel shader which is used with the stream processing algorithm described in "General-purpose computation on graphics hardware". The shader is executed for each pixel of the render target by rendering a screen-sized quad. The current render target is set to one of the double buffer velocity textures. The other texture of the double buffer is used as input data stream and contains the velocities from the previous time step. Other particle data, either from inside the attribute textures or as general constants, is set before the shader is executed.

There are several velocity operations that can be combined as desired (cf. [Sims1990] and [McAllister2000]): global forces (e.g. gravity, wind), local forces (attraction, repulsion), velocity dampening, and collision responses. For our GPU-based particle system these operations need to be parameterized via pixel shader constants. Their dynamic combination is a typical problem of real-time graphics. It is comparable to the problem of light sources and material combinations and can be solved in similar ways. Typical operation combinations are to be prepared in several variations beforehand. Other operations can be applied in separate passes, as all operations are completely independent.

Global forces, e.g. gravity, influence particles regardless of their position with a constant acceleration in a specific direction. The influence of local forces however depends on the particle's position which is read from the position texture. A magnet attracting or repelling a particle has a local acceleration towards a point. This force can fall off with the inverse square of the distance or it can stay constant up to a maximum distance (cf. [McAllister2000]). A particle can also be accelerated towards its closest point on a line, leading to a vortex-like streaming.

A more complex local force can be extracted from a flow field texture. Since texture look-ups are very cheap on the GPU, it is quite efficient to map the particle position into a 2D or 3D texture containing flow velocity vectors. This sampled flow vector v_fl can be used with Stoke's law of a drag force F_d on a sphere:

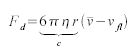
where n is the flow viscosity, r the radius of the sphere (in our case the particle) and 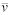the particle's velocity. The constants can all be combined to a single constant c , for efficient computation and for simpler manual adjustment.

Global and local forces are accumulated into a single force vector. The acceleration can then be calculated with Newtonian physics:

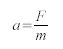
where a is the acceleration vector, F the accumulated force and m the particle's mass. If all particles have unit mass, forces have the same value as accelerations and can be used without further computation.

The velocity is then updated from the acceleration with a simple Euler integration in the form:

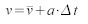
where v is the current velocity, 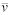the previous velocity and 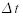the time step. Another simple velocity operation is dampening, i.e. a scaling of the velocity vector, which imitates viscous materials or air resistance. This is basically a special case of equation 1 with a flow velocity of zero. The reverse operation, an undampening, can be used to imitate self-propelled objects, e.g. a bee swarm.

A more important operation is collision. Collision with complex polygonal geometry is hardly practical on current GPUs, whereas collision with a plane or bounding spheres is rather cheap. The real strength of collision on the GPU however is collision against texture-based height fields that are typically used to model terrain. By sampling the height field three times a normal can be computed which is then used for calculating the reflection vector. The normal can also be stored in the height field, basically making it a scaled normal map.

If a collision has been detected, the collision reaction, i.e. the velocity after the collision, has to be computed (cf. [Sims1990]). First the current velocity has to be split into a normal and a tangential component. If n is the normal of the collider at the collision point, these can be computed as:

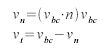
where v_bc is the velocity computed so far, i.e. before the collision occurs, v_n is the normal component of the velocity and v_t the tangential one. The velocity after the collision can now be computed with two further parameters describing material properties. Dynamic friction 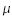reduces the tangential component, and resilience 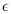scales the reflected normal component. The new velocity is computed as:

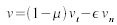
This default handling of the collision however has two problems which cause visual artifacts. The slow-down effect of the dynamic friction will lead to situations where the velocity is (very close to) zero. Since in our case the collision is processed after acceleration forces like gravity, this might lead to particles hanging in the air. They virtually seem to be attached to the side of a collider, e.g. at the equator of a sphere collider with respect to the global gravity. Therefore the friction slow-down should not be applied if the overall velocity is smaller than a given threshold.

The second problem is caused by particles getting caught inside a collider. A collider with sharp edges, e.g. a height field, or two colliders close to each other might push particles into a collider. This can be avoided by trying to push a caught particle out of the collider. Normally, the collision detection is done with the expected next particle position to avoid the particle from entering an object for the time of one integration step (cf. figure 2a). The expected particle position p_bc is computed as

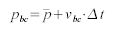
where 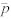is the previous position. Doing the collision detection twice, once with the previous and once with the expected position, allows differentiating between particles that are about to collide and those having already penetrated (see Figure 2b). The latter can then be pushed out of the collider, either immediately or by applying the collision velocity without any slow-down. The direction of the shortest way out of the collider can be guessed from the normal component of the velocity:

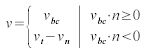
3. Update Positions

The second part of the particle system simulation updates the position of all particles. Here we are going to discuss the possible integration methods in detail that have been mentioned earlier (cf. "Particle data storage"). For the integration of large data sets on the GPU in real-time only simple integration algorithms can be used. Two good candidates for particle simulation are Euler and Verlet integration. Euler integration has already been used in the previous section to integrate the velocity by using the acceleration. The computed velocity can be applied to all particles in just the same way. This leads to

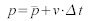
where p is the current position and 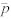the previous position.

In some ways even simpler than Euler integration is Verlet integration (cf. [Verlet1967]). Verlet integration for a particle system (cf. [Jakobsen2001]) does not store the velocity explicitly. Instead, the velocity is implicitly deduced by comparing the previous position to the one before. The great advantage of this handling for the particle simulation is that it reduces memory consumption and removes the velocity update rendering pass.

If we assume the time step is constant, the combination of the velocity and position update rules from the Euler integration can be combined to a position update rule based only on the acceleration:

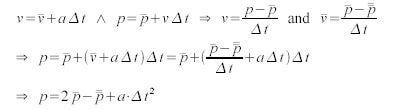
where 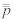is the position two time steps ago. Verlet integration handles simple (global or local) acceleration forces quite efficiently. However, complex velocity operations, like the collision reaction discussed above, require position manipulations to implicitly change the velocity in the following frames. Alternatively, collision can be handled more efficiently with position constraints that simply move the position out of the collider. Due to the deduction of velocity based on this constraint movement, an implicit reflection velocity is set. Other constraints can be used to limit the distance between a pair or group of particles, which is useful for particle simulation of cloth or hair (cf. [Jakobsen2001] for more details).

4. Sort for Alpha Blending

If particles are alpha blended, a distance-based sorting should be applied or else particles in the front will not be blended correctly with particles behind them. This error might be intolerable depending on the size and amount of the partially transparent pixels of each particle. Due to the cost of sorting, first examine whether these particles can instead be rendered with a commutative blending function, e.g. additive or multiplicative.

A particle system on the GPU can be sorted quite efficiently with the parallel sorting algorithm “odd-even merge sort” [Batcher1968]. It is independent of the data's sortedness, i.e. it always has a constant number of iterations for a data set of a given size. This is important as the parallel hardware execution makes it inefficient to check whether all data is already in sequence. This algorithm also guarantees that with each iteration the sortedness never decreases. If you assume a high frame-to-frame coherence, this property allows you to distribute the whole sorting sequence over 20 - 50 frames. Especially game applications often know the maximum velocity with which the viewer and the particle objects can move, so assumptions about the rate of change in the sortedness can be made.

The basic principle of odd-even merge sort is to divide the data into two halves, to sort these and then to merge the two halves (for further details cf. [Lang2003]). The algorithm is commonly written recursively and in a serial way, but a closer look at the resulting sorting network shows its parallel nature. Figure 3 shows the sorting network for eight values, an arrow marking a comparison pair. The first arrow indicates that element 0 is compared to element 1 and possibly swapped in case the order is not fulfilled. You can see that several consecutive comparisons are independent of each other. They can be grouped for parallel execution, which is indicated here by the vertical lines.

Figure 4 shows the Cg (cf. [Mark2003]) code for the sort passes. The code can be ported to Microsoft HLSL (cf. [Microsoft2002]) by simply mapping the texRECT instruction onto a tex2D instruction. The code is slightly simplified for readability and sorts only a one dimensional texture. To enhance the shader for sorting two dimensional textures the texel index needs to be split into u and v coordinates before look-up. The sorting has two alternative sort shaders, a “recursion” and an “end” step. The pseudo code to trigger the sort passes on the CPU is shown in figure 5.

The sorting requires 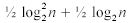passes, where n is the number of elements to sort. For a 1024x1024 texture this leads to 210 rendering passes. Just like in the particle simulation, they always render the full texture into a render target using a double buffer. As mentioned earlier, running all 210 passes each frame is far too expensive on current hardware, but spreading the whole sorting sequence over 50 frames, i.e. 1-2 seconds, reduces the workload to only four passes each frame, which results in acceptable performance.

This general sorting algorithm is applied to the particle simulation in the following way: The sorting data textures contain the particle-viewer distance and the index of the particle. The distance in this texture is updated after the position simulation. After sorting the rendering step (cf. next two sections) looks up the particle attributes via the index in this texture.

5. Transfer Texture Data to Vertex Data

The copying of position data from a texture to vertex data is a hardware feature that is only just coming up in PC GPUs. Currently there are two approaches to this problem:

1. DirectX and OpenGL offer vertex textures with the vertex shader (VS) version 3.0 (cf. [Microsoft2002]) rsp. the ARB_vertex_shader extension (cf. [OpenGL2003]). While vertex textures would be rather optimal for this technique, at the time of writing there is no hardware supporting this feature.

2. The alternative solution uses"uber-buffers" (also called super buffers; cf. [Percy2003]) which basically are a data-agnostic storage of vertex or pixel data in a buffer. This concept is already available in current GPUs, but it is up to now only supported by the OpenGL API. The current implementation uses OpenGL with the vendor specific NV_pixel_data_range extension (cf. [NVIDIA2002]) which offers accelerated asynchronous copying of data inside the GPU memory. Since the data can be copied from pixel to vertex memory, this is a basic implementation of the uber-buffer concept.

The particles can be rendered as point sprites, triangles or quads (cf. next section). If multiple vertices per particle are to be generated, the currently used uber-buffer concept for data transferal requires manual replication of the particle position before rendering. In a further rendering step the positions need to be rendered three or four times into pixels lying next to each other in a texture. To avoid this overhead, the current implementation uses point sprites.

Two upcoming concepts in future hardware can handle this replication problem more efficiently: The so-called "vertex stream frequency" is about to be introduced on hardware supporting the VS3.0 version. This feature allows reducing the update frequency of vertex input data to a vertex shader. Basically, one entry in a vertex stream can be used for a range of several consecutive vertices, whereas other vertex streams change at a different rate. The replication problem will also be solved once vertex textures are used, as they are actively read by a shader that otherwise uses static vertex data. This static vertex data contains the index of a particle to be read from the texture; it can already be replicated several times.

6. Render Particles

Finally, the transferred vertex positions are used to render primitives to the frame buffer in a traditional way. For the reasons mentioned in the previous section and in order to reduce the workload of the vertex unit, particles are currently rendered as point sprites. Compared to rendering single triangles or quads this reduces the number of vertices to a third or a quarter. The disadvantage though is that particles are always axis-aligned and do not have a 2D rotation about the screen space z axis. To overcome this limitation, a 2D rotation is applied to the texture coordinates inside the pixel shader. The decision about using point sprites or generating triangle/quad geometry is to be made depending on the distribution of workload between vertex and pixel units of a particular application.

During the rendering other attributes (e.g. color and size) are computed inside the vertex shader from the particle type parameters (cf. "Particle data storage"). Some of them take into account the relative age of the particle or a pseudo-random function.

The current implementation uses the following computation rules for these particle attributes: The size of a particle is random within a range that is defined by the particle type. The initial orientation and a rotation velocity (2D in screen space) are also determined randomly within a defined type-based range.

Based on the relative age of the particle the color and opacity are interpolated from four keyframes. These keyframes are defined for each particle type and need not be equidistant. They define three linear function segments that are first converted into a form for efficient GPU evaluation and then uploaded with the particle type data.

It is not possible to switch textures on a per-particle basis while rendering. Thus it is necessary to combine different textures into tiles of a larger 2D texture. Each particle then modifies the texture coordinates appropriately. If point sprites are used, the texture coordinates will be generated automatically by the rasterizer in the range [0..1]². The sub-texture selection then needs to be done in the pixel shader. Fortunately, the texture coordinate transformation for the 2D rotation we described above will do the sub-texture selection basically for free, as a transformation by a 2×2 or by a 3×2 matrix both need two vector instructions.

Conclusion

Of course processors are never fast enough, so up to now the implementation on the first generation of floating point GPUs simulates and renders a 1024×1024 texture of particles in real-time only with few effects and without sorting. Sharing the GPU with other techniques and using the full feature set currently allows up to 512×512 particles. The performance is expected to improve significantly with the upcoming generation of PC graphics hardware.

This paper has shown how to design and implement a state-preserving physical particle simulation on current programmable graphics hardware. The simulation can use either Euler or Verlet integration to update the particle positions. Other particle attributes are simulated with less complex algorithms. Without permanent storage they are always evaluated on demand. Additionally, an efficient parallel sorting algorithm for particles has been introduced.

The main strength of GPU-based particle systems is the low cost of individual operations on the data set. Once a basic algorithm is implemented, endless ideas for manipulating velocity and position come up and are easily implemented in higher level shading languages. New, yet unimplemented ideas include e.g. collision with arbitrary geometry and local forces being attached to the particles themselves. These forces basically lead to a second order particle system (cf. [Ilmonen2003]).

Other topics for further discussion are the application of the algorithm to constraint PS (e.g. to simulate cloth or hair) and its modification for other rendering techniques instead of individual geometry.

The only part of the particle simulation remaining on the CPU is the allocation and deallocation of particles as these do not map well to current parallel hardware. Future graphics hardware might support simple allocation algorithms with special-case serial registers that could be used as stack pointers.

Further research should also be done on improving the exploitation of frame-to-frame coherence by the sorting algorithm. Currently, the full sorting sequence of the algorithm is divided evenly over several consecutive frames. Since the sorting result is not necessarily exact, it is possible that certain parts of the sorting sequence are visually more important than others and ought to be executed more often.

How applicable to upcoming video game console hardware the introduced state-preserving particle simulation is, remains to be seen. But the trend towards increased multi-processing hardware is a good indication that the parallel computation of particle systems will grow in importance.

Acknowledgments

I would like to thank my colleagues at Massive Development, especially Ingo Frick, Dr. Christoph Luerig and Mark Novozhilov, and Prof. Andreas Kolb from the University of Siegen for the fruitful discussions and support in writing this paper. I also thank very much Sieggi Fleder for never giving up on my Germanic English. Furthermore, I am grateful to Matthias Wloka and his colleagues at NVIDIA, who helped the demo implementation to stay on the cutting edge of technology.

References

Batcher1968: Batcher, Kenneth E.; Sorting Networks and their Applications. In Spring Joint Computer Conference, AFIPS Proceedings 1968

Buck2003: Buck, Ian; Data Parallel Computing on Graphics Hardware, 2003,
http://graphics.stanford.edu/~ianbuck/GH03-Brook.ppt

Burg2000: van der Burg, John; Building an Advanced Particle System, Game Developer
Magazine, 03/2000

GPGPU2003: Harris, Mark et al.; GPGPU Website, 2003-2004, http://www.gpgpu.org/
Green2003: Green, Simon; Stupid OpenGL Shader Tricks, 2003,
http://developer.nvidia.com/docs/IO/8230/GDC2003_OpenGLShaderTricks.pdf

Harris2003: Harris, Mark, Real-Time Cloud Simulation and Rendering, Department of
Computer Science, University of North Carolina at Chapel Hill, 2003

Ilmonen2003: Ilmonen, Tommi; Kontkanen, Janne; The Second Order Particle System. In WSCG Proceedings 2003

Jakobsen2001: Jakobsen, Thomas; Advanced Character Physics. In GDC Proceedings 2001

Lang2003: Lang, Hans W.; Odd-Even Merge Sort, 2003, http://www.iti.fhflensburg.de/lang/algorithmen/sortieren/oemen.htm

Mark2003: Mark, William R.; Glanville, R. Steven; Akeley, Kurt; Kilgard, Mark J.; Cg: A System for Programming Graphics Hardware in a C-like Language. In SIGGRAPH Proceedings 2003

McAllister2000: McAllister, David K.; The Design of an API for Particle Systems, Technical Report, Department of Computer Science, University of North Carolina at Chapel Hill, 2000

Microsoft2002: Microsoft Corporation; DirectX9 SDK, 2002, http://msdn.microsoft.com/directx/

NVIDIA2001: NVIDIA Corporation; NVIDIA SDK, 2001-2003, http://developer.nvidia.com/

NVIDIA2002: NVIDIA Corporation; OpenGL Extension NV_pixel_data_range, 2002,
http://oss.sgi.com/projects/ogl-sample/registry/NV/pixel_data_range.txt

OpenGL2003: OpenGL ARB; OpenGL Extension ARB_vertex_shader, 2003,
http://oss.sgi.com/projects/ogl-sample/registry/ARB/vertex_shader.txt

Percy2003: Percy, James; OpenGL Extensions, 2003,
http://www.ati.com/developer/SIGGRAPH03/Percy_OpenGL_Extensions_SIG03.pdf

Purcell2003: Purcell, Timothy J.; Donner, Craig; Cammarano, Mike; Jensen, Henrik W.;
Hanrahan, Pat; Photon Mapping on Programmable Graphics Hardware. In Graphics Hardware Proceedings 2003

Reeves1983: Reeves, William T.; Particle Systems – Technique for Modeling a Class of Fuzzy Objects. In SIGGRAPH Proceedings 1983

Sims1990: Sims, Karl; Particle Animation and Rendering Using Data Parallel Computation. In SIGGRAPH Proceedings 1990

Verlet1967: Verlet, Loup; Computer Experiments on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules, Physical Review, 159/1967

______________________________________________________