Deep Dive: Physics-based animation in Gibbon: Beyond the Trees

Hi, I’m Eddy Boxerman, a physics/animation/gameplay programmer & designer. Gibbon: Beyond the Trees, a game I’ve been collaborating on over the last few years with the awesome folks at Broken Rules, came out on Apple Arcade a few weeks ago.

It’s an endless-runner style game in which the player controls a gibbon that can swing, slide, and somersault their way through the jungle, and beyond. It’s a beautiful game, not only visually, but aurally and narratively as well. (I may be biased).

One of the things people have been remarking on is the game’s “fluid animation,” so we thought it’d be fun to write about that, as we definitely put a lot of work into that aspect. Here I’ll focus on the game’s procedural animation (what’s seen during gameplay) as opposed to the wonderful cut-scene animations, created by Simon Griesser and ingeniously integrated into the game by Vivien Schreiber.

The first thing you need to know is this: gibbons are amazing. If you’ve never seen a gibbon “brachiate” (swing from handhold to handhold), watch the below video.

Such fluid swinging is what inspired Felix to try to create a game that would convey the sense of joy and freedom-of-movement that gibbons must feel.

He began working on a prototype, but found the movement to be quite complex, and elusive to capture, so he branched out…

Animation mockups can be a great way to explore and sketch out a game’s identity, without requiring it to be fully built. So Felix and Clemens worked with their office-mate, Sascha Vernik, to create the following mockup:

They also asked David Rosen of Wolfire Games if he’d be interested in creating a movement prototype of gibbon brachiation, running, and sliding. (David has a long history of creating cool, procedural animation systems, such as for their game Overgrowth.) Luckily he was up for the challenge, and created a system that was an awesome launching point for creating the full game. David also just published a video describing that prototype and the techniques he employed therein – required viewing for anyone interested in the subject!

I also joined the project around this time, and started to work with Felix on fleshing all this out into a playable game prototype. Our next steps were to build a simple game world of branches, canopies, and vines, and have our gibbon start to move through it. Felix hit the world & level building, and I got to work on having the gibbon move through this more complex terrain.

An early capability we needed to give our procedural gibbon was the ability to transition from flying through the air, to swinging. (Prior to this, it could go from flying to running, and running to swinging, but not flying to swinging.) So I added this. But in doing so, I started to bump into some of the limitations of modeling swinging as a sine-wave. Questions arose, such as how to set the amplitude, frequency, and phase depending on the gibbon’s incoming velocity. Also questions about how to pose/pull the arms to get a decent sense of initial contact. I tried to connect things up, and it looked ok some of the time, but sometimes it looked kinda glitchy, and momentum often didn’t feel like it was being conserved. And as we built out our trees and world, we found that this kind of transition happened very often, as did “launches” (releasing from swinging), which also felt quite discontinuous and unphysical.

So I felt we needed a swinging model that centred around handholds, to achieve nice transitions into and out of swinging. This was especially true in cases where our gibbon would do a single swing, on eg. a vertical branch, with no long-term sine-wave to follow.

a tracing of a single gibbon swing, from [1]

So I tried a quick experiment, modeling our gibbon as a two-point rig – a hand and COM (center-of-mass) – to see how a handhold-centred approach to swinging could feel.

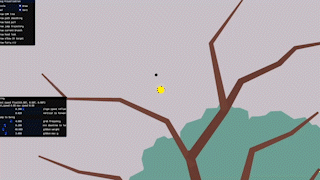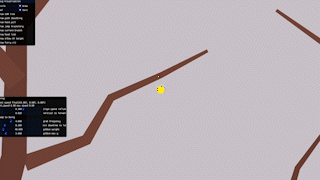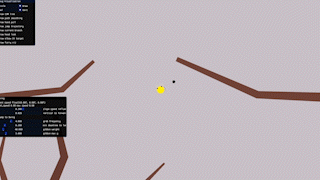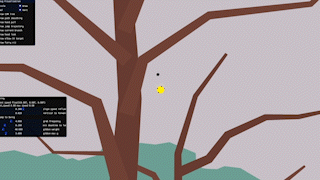
Despite the crude model, I liked the sense of contact and momentum transfer this approach gave. For instance, when falling from a great height, the gibbon’s swing naturally converts their downward speed into some fast forward motion.

As for modeling a gibbon as a “furry ball” with an arm sticking out, that didn’t seem like such a poor simplification given videos like this:

Something else emerged from this approach that I hadn’t initially thought about; but as I read papers on the subject (this one in particular) and watched videos of gibbons swinging, it became clear there was a strong relationship between a gibbon’s velocity and where it wanted its next handhold to be. Specifically, gibbons ideally want their “grab arm” to be reaching out perpendicularly to their velocity. In this way, the swing is initiated smoothly, with no discontinuities in the gibbon’s COM velocity – just a new (perpendicular) force applied, causing a smooth rotation. Anything else causes a “collisional energy loss”, and possibly some serious arm strain or whiplash.

Gibbons ideally want their “grab arm” to be perpendicular to their velocity

I should note that, given the high speeds in our game, I focused on “ricochetal” brachiation, in which there’s an aerial phase between handholds, and things behave quite elastically. Real gibbons also use “continuous contact” brachiation, at slower speeds, for which the COM-path looks different; but we weren’t really operating in that regime. Anyways, it seems this idea of minimizing collisional energy loss is a key in “understanding locomotion using limbs in any terrestrial environment.” [1] The upshot is this gave clear guidance on where a gibbon should be looking for handholds at any given instant, as well as what pose a gibbon adopts in the air as they approach a handhold. Useful knowledge for a procedural animation system! (You may have noticed this detail in where the black-dot “hand” is in the video above – constantly adjusting based on velocity.)

On the downside, this system didn’t really plan ahead, treating all swingable points as equal, regardless of what tree or branch the handhold was on. This ran counter to Felix’s vision for the project. He wanted the game to feel smooth and intuitive, with gibbons brachiating along the lengths of branches “automatically”, almost like a flowy rhythm game – not twitchy, requiring players to give input for every handhold. This made perfect sense. It was important both from a gameplay perspective, so that players could relax and predict where they were going as they followed a branch, and in terms of realism – gibbons generally swing along branches; they don’t treat the jungle as a disconnected scattering of handholds.

At this stage I wasn’t sure how to solve the ballistic-planning problem (more on that later) of getting this handhold-centred system to always follow branches. So I combined the two, using this new “free-swing” system for single swings and swing initiation (first grab from the air), and blending that into the sine-wave system for subsequent brachiation until the end of a given branch. Here’s how that looked.

Still rough, but it worked. As you can see, I was using the free-swing for canopies and for vines (modified) as well, which made pursuing this approach all the more compelling. (I had also done a first pass on deformable trees and vines at that point, but to stay focused here I’ll leave those details for another time.)

A general topic I’d like to point out here is the whole LOD (level of detail) approach to procedural animation. David’s approach of modeling the COM, then “mapping” that to the 5-point rig (which was a fantastic design choice), then mapping that (including some inverse kinematics) to a “complete”, 14-point rig, and finally mapping that to the display rig’s bones (including joint rotations), was a great structure to work with. It provides a certain simplicity and abstraction at each level, allowing the “procedural animator” to focus on the important aspects at that level, without the system becoming too complex. And as we move upwards, the pieces that were computed at lower levels become constraints on the higher LODs, making sure the important movements (like COM continuity, hand contact, etc.) don’t get lost. It’s a sweet combination, allowing for both control and nuance. In particular, it allowed me to add the 2-point swinging rig into the LOD chain in a very natural way.

Before I go on, there’s one more free-swing experiment I’d like to share, in which I allowed the gibbon to move right-to-left as well, going back and forth on the same branch. We didn’t use this, as it didn’t fit the game, but it was fun to watch.

Ballistic Planning

Next, I wanted to try to solve the “ballistic planning” problem, so I could use the free-swing approach for all swings, while still following a branch. The idea would be to have a two-phase brachiation system: a swing phase and a ballistic phase. The gibbon would (1) grab a handhold at some incoming velocity and angle; (2) swing on it until a given release angle; (3) fly ballistically (ie. under gravity) until coming to the next handhold, and repeating the loop until the end of the branch. Here’s some simple example geometry to visualize this.

Sounds simple enough, but the key was to connect the release (2) of each swing (its angle and speed) so the gibbon would end its ballistic trajectory with its hand at the next, chosen/planned handhold, and with its velocity perpendicular to its grab-arm vector. And while we have some flexibility in setting the launch speed, we wanted things to look smooth and natural, so we had to avoid any strong boosts or slowdowns. We also wanted to keep the gibbon’s speed between some upper and lower thresholds, so the gibbon wouldn’t stall, or start flying super fast.

To give some intuition about this problem, consider that for speeds below some threshold, there is no solution. Beyond that, there’s an infinite range of solutions. Regardless, even for a given, valid speed, I couldn’t find an analytic solution to the problem. (ie. no closed form equation that you can just plug some numbers into and get an answer, such as release angle, out.)

So, as I learned in computer science when facing a tricky-to-solve optimization problem, I went with a stochastic approach: guessing, scoring, and picking the best option. I also used an iterative approach to refine each guess.

I’d start by randomly picking (in a desired range) an average COM-speed for the arc, a launch angle, and a grab angle. This would allow me to compute the COM positions at release and at grab. Based on that I could compute flight time, and launch velocity required. This in turn allowed me to compute a new, refined release angle and grab angle (based purely on velocities), which in turn gave me new COM positions, etc, etc. After about five to ten iterations of this, the calculation would converge (as I had hoped when designing the algorithm), and I’d have an accurate arc for that speed.

I would then score that arc, based on some desired parameters. For instance, some of these guesses would give some pretty crazy, high arcs. These would get a bad score. I’d also significantly penalize the score of a solution that required a significant change in the gibbon’s momentum during their swing from positions (1) to (2). Some “muscle work” was ok – even good, depending on what we wanted for gameplay purposes – but too much looked discontinuous, as though our gibbon had gotten a rocket boost, or hit a wall.

After a bunch of these stochastic, iterative solutions, I’d pick the one with the best score, and voila: a “good” solution! Hopefully, anyways. I did end up tweaking the ballistic planner’s scoring function from time to time over the next 1.5 years of the project! (To pick more preferable solutions, and sometimes adding strong penalties to avoid some extreme edge cases.)

Of course, things never quite line up perfectly. I had to allow for some tolerances in all these systems: grabs where they aren’t ideal (but where players still expect them), vectors not being quite perpendicular, arm-bend/stretch, etc. The code required some extra variables here, some blends there, a little accounting to re-inject any lost energy (except where we intentionally bleed speed), some velocity “projection”, etc. Various devils in the details.

Sometimes I wondered if I was going too far down this rabbit hole. Don’t get me wrong: I do enjoy this kind of problem. But projects have finite budgets, and I wasn’t always sure if this kind of improvement was “worth it”. But on the whole I felt it was – especially in our increasingly complex levels with branches of various lengths (short and long) to traverse. That said, I wanted to do an apples-to-apples comparison; so I went back to David’s original test scene, the one with the gibbon traversing that “infinite” terrain, to see how they compared in that context. Here’s the before and after:

original sine-wave brachiation

new two-phase, ballistic brachiation (+ fancy new model from Simon!)

In this “infinite swinging” context, with no discontinuities to deal with, it wasn’t as big an improvement, but it still felt more natural and physical to me. I’m curious to hear what others think.

Conclusion

After “basic” brachiation, and as the team and project expanded, we continued to work on a number of animation, physics, and gameplay fronts. I could dive into the details around vine swinging, canopies, and cables; also backflips, bouncing, and pair throws(!); our air-planner and contextual controls; our “friend AI”; the 2.5D nature of the game; blending procedural and artist/fbx animations and poses; bird flight and quadruped monkey-running; etc. I’ll save those details for another time, though I’d be happy to hear if any of those are of particular interest.

For now, I’ll just sign off with a snippet of how the game looked when we shipped it last week:

Thanks for reading! And as always, questions and feedback are welcome.

[1] New Perspectives on Brachiation Mechanics, John E.A. Bertram