Game Developer Deep Dives are an ongoing series with the goal of shedding light on specific design, art, or technical features within a video game in order to show how seemingly simple, fundamental design decisions aren’t really that simple at all.

Earlier installments cover topics such as how art director Olivier Latouche reimagined the art direction of Foundation, how the creator of the RPG Roadwarden designed its narrative for impact and variance, and how the papercraft-based aesthetic of Paper Cut Mansion came together with the developer calls the Reverse UV method.

In this edition, Tim FitzRandolph of Toyful Games gives an illuminating look into the soft body physics simulation of JellyCar Worlds, aiming to lightly educate on the basics to inspire similar simulations. 

Hi, I’m @walaber, an independent developer, most well-known as the creator of the JellyCar series of games. On the occasion of the much overdue release of JellyCar Worlds (my modern sequel that updates and improves JellyCar for modern platforms), I’ve decided to finally spend some time sharing the details about how the soft-body physics simulation works in the game, which gives the game its unique charm and gameplay.

JellyCar is powered by a custom soft-body (only!) physics engine, which enables all of the gameplay features and interactions. In this article, I will explain each element involved in creating a simulation like the one in JellyCar Worlds, as clearly and visually as possible. This isn’t a full-blown step-by-step tutorial, so don’t expect code snippets. Instead, this should familiarize you with the main concepts, give you a starting point for your own investigations into similar physics simulations, and hopefully inspire you to try making some physics-based gameplay of your own.

It’s All Just a Bunch Of Points

Rigid body simulations usually operate on the idea of a small number of “bodies,” which are then composed of many “colliders.” Colliders are often various primitives like cubes, spheres, capsules, and perhaps convex hulls derived from meshes.

By contrast, the 2D soft-body system in JellyCar is kind of the opposite: we have many, many individual bodies that move around, and their aggregate positions are used to define the shape (“collider”) of the object.

These “bodies” are usually referred to as point masses, as they are a single point with a mass (“weight”) that can move around as a result of forces. So, the first step in building a soft body simulation is to get a bunch of point masses that can accumulate forces, and integrate those forces into changes in velocity and changes in position. In other words, a bunch of points that you can push around and they move. At this point, you might have something that looks like this: a bunch of dots that can fall with gravity.

This doesn’t look like much, but it’s the heart of the entire simulation! Nearly everything we do past this point will simply be various ways to produce forces that act on these points to make them move as soft, squishy objects.

Shapes and Collision Detection

The next step (and by far the most daunting) is to connect these points into individual shapes (each point represents a “vertex” or corner on the shape), so that they can act together like a larger single object (a “soft body.”) Defining the shape is very simple! We create a new concept called a “soft body,” and its shape is simply a list of point masses. Connecting these point masses in order defines the shape of the body:

Now comes the hard part: detecting collisions between two shapes! After all, we won’t have much gameplay if we can’t have our soft bodies collide, push, and squish each other. Collision detection is a deep and often difficult topic, but luckily for our purposes we can create a simplified system. It hinges on this realization: when our soft bodies collide, we will need to respond by moving and adjusting velocities on the individual point masses involved.

Also, it’s a soft body system, we actually want our objects to deform, so we don’t need to figure out how to move entire shapes to resolve overlap, we can just move the offending points where an overlap is happening, and let the body deform as a result!

In essence, this means that we can simplify the problem quite a bit. In JellyCar’s system, collision detection looks like this:

Given a potential collision between objects A and B:

And that’s basically it! Let’s break this down into separate problems. First: how to know if a point is inside the other body’s shape. This is essentially asking if a point is inside a closed polygon. Luckily this is a well-researched problem, and many solutions exist. The method I used in JellyCar is this:

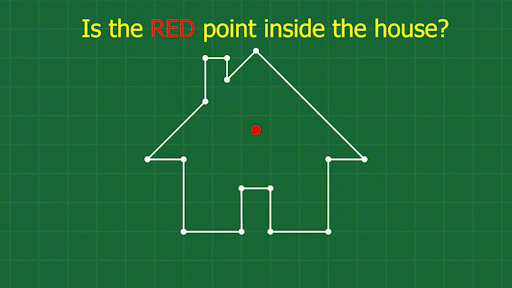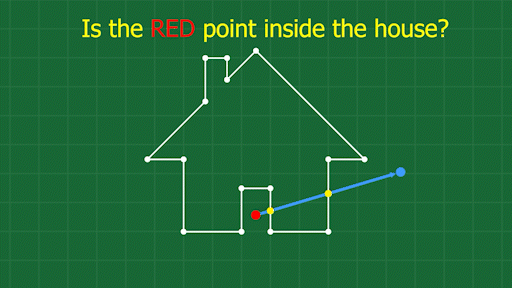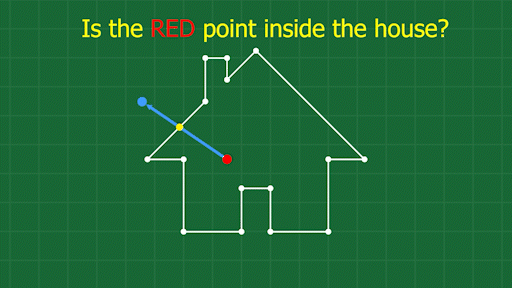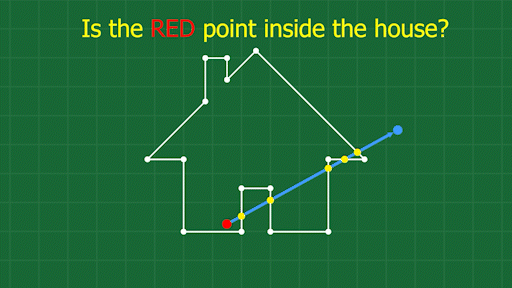
Find a point you know is outside the shape. Draw a line between your test point, and the outside point. Count up the number of times this line crosses the shape. If the number is odd, the test point is inside the shape. If the number is even, the test point is outside the shape. Note that this algorithm only works for polygons without self-intersections.

Collision Resolution

Now that we know our test point is inside the other object’s shape (polygon), we need to get it out! Because the fundamental building blocks of our simulation are the point masses at each corner, our solution needs to involve moving some amount of point masses. It works like this: find the closest point on the shape to our test point. This will give us a direction to move the test point to get it out of the shape, and also the edge (2 points) on the shape that it is closest to.

Now we can move all 3 points just enough to get the point outside of the shape. How much we move the points is based on the relative mass between all 3 points and also where along the edge we are.

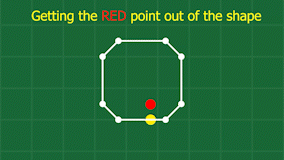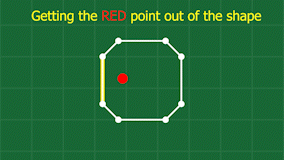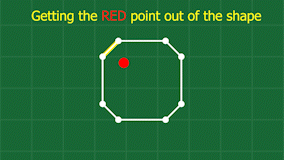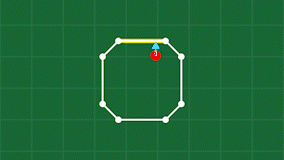
We also need to adjust the velocities of the points involved, since a collision has taken place, and things like friction and their relative velocities need to be accounted for. When I was coding this, I had no idea how to resolve a collision between a point and a line, so I came up with a simple approximation. I imagine the edge is actually just another point, placed at the exact spot to produce the same normal between the test point and the edge. Then I use the standard maths for an inelastic collision between two perfect spheres (imagine billiard balls). This gives me a starting place for the resulting velocities from the collision, which I then adjust a bit based on the desired friction between the materials involved. Finally, I take the resulting velocity for the virtual point that represents the edge, and distribute it back to the 2 points on that edge, and we’re done!

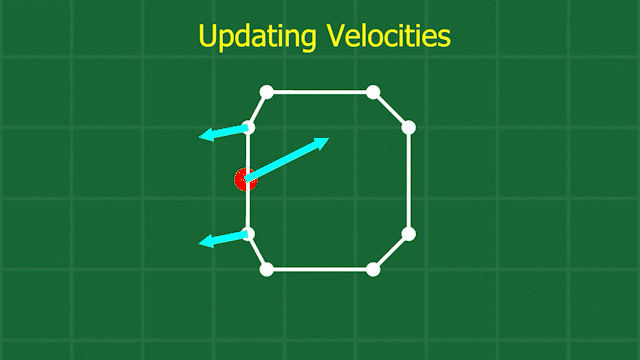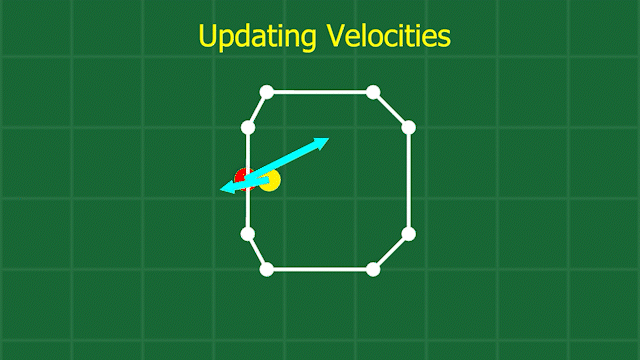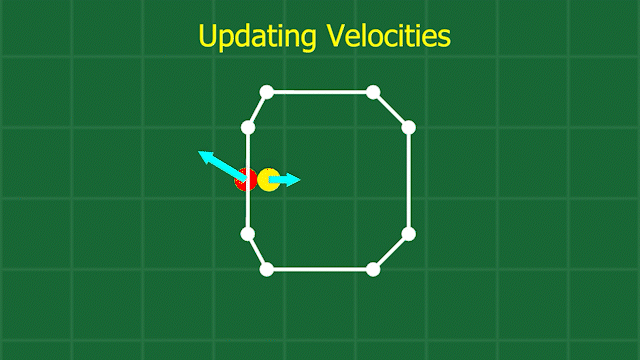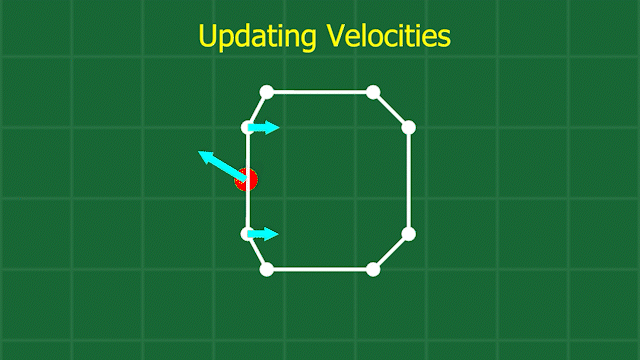
Now we have handled the scary part of our simulation, and shapes can now collide and resolve their collisions. Check it out, it’s amazing:

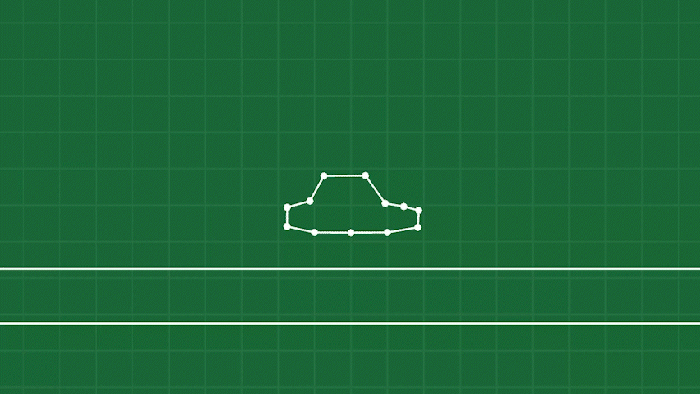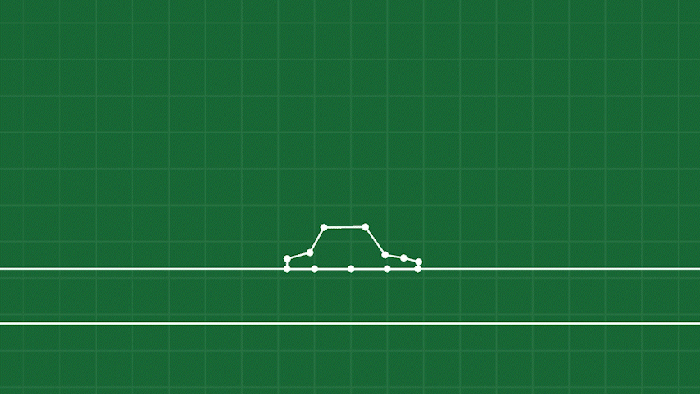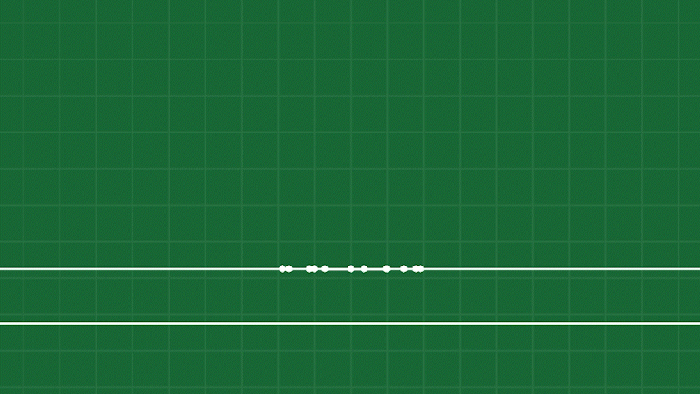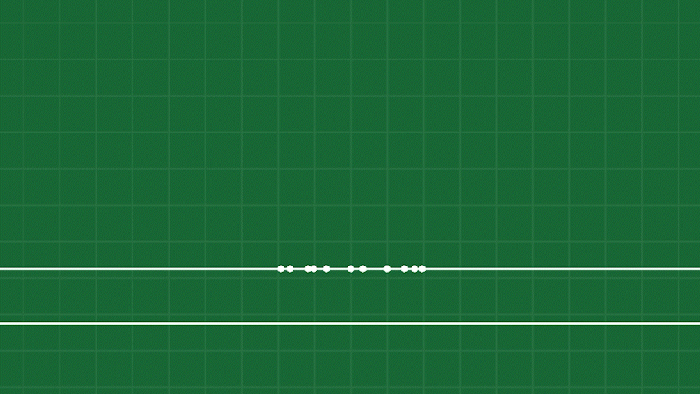
OK maybe not yet. We don’t have anything causing these objects to maintain their shape! Which brings us to…

Springs

The main tactic to have the bodies keep their shape while allowing satisfying deformation is springs. A spring is really just a force that acts on two Point Masses, trying to keep them a specific distance apart from each other. Too close? Apply a force that pushes them apart. Too far? Apply a force that pulls them together.

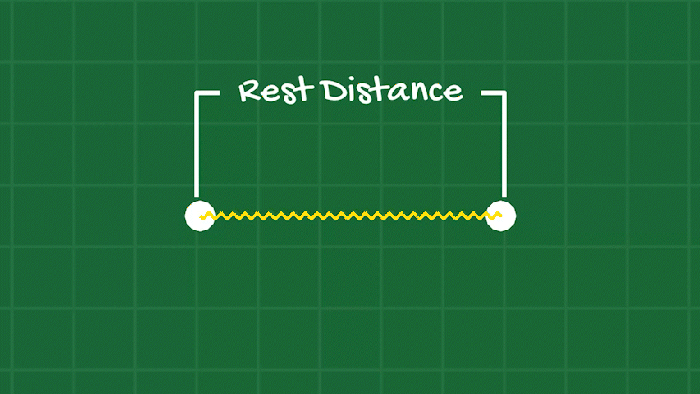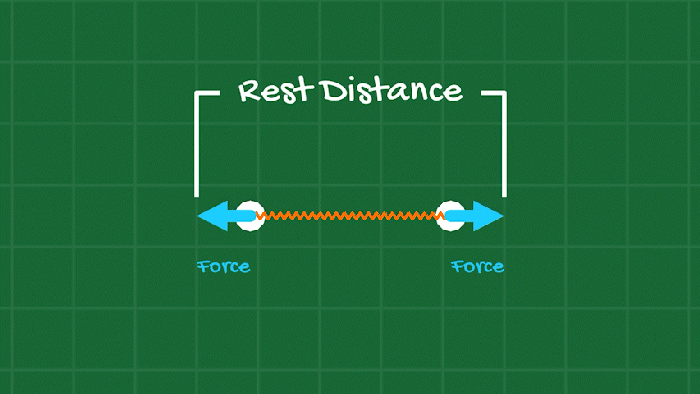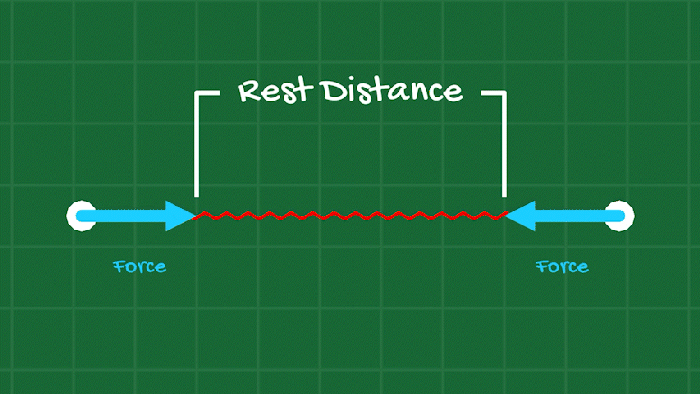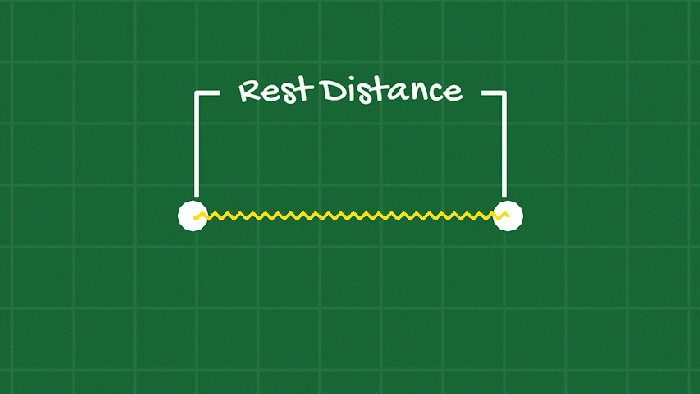
We can add springs between the points all around the object’s shape (its “edges”), and also add internal springs (kind of like building a bridge) to give the object some structure.

This goes a long way, and we now basically have a working soft body simulation, check it out!

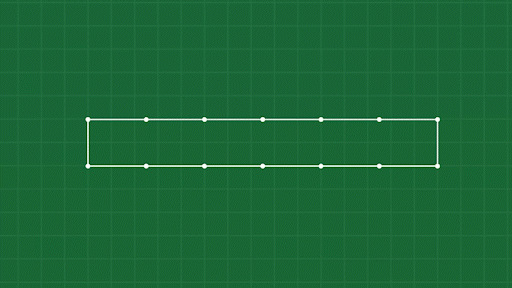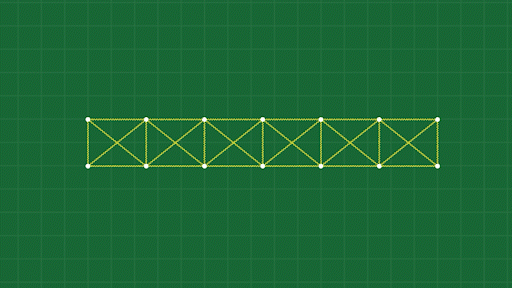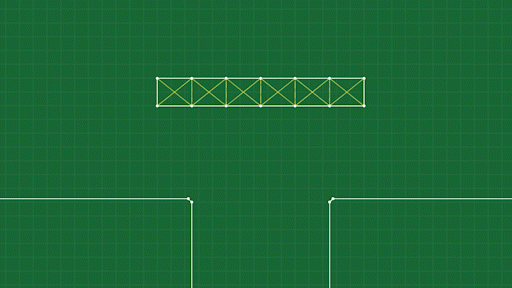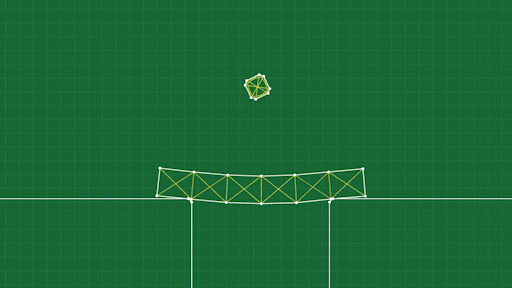
When an object deforms, the springs are compressed, and then they push on the points to try and get back to their original shape.

Once you start making gameplay with this system, you might start running into some issues with objects “popping inside out”. This is a side effect of the springs: they have no concept of orientation, they just want to maintain distance. A common example of this is with long, thin objects like you see below:

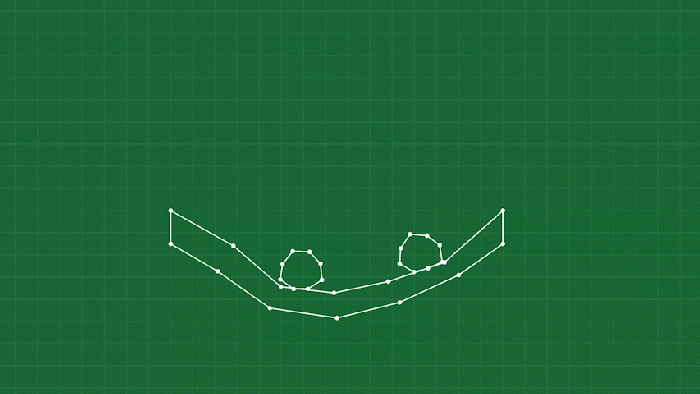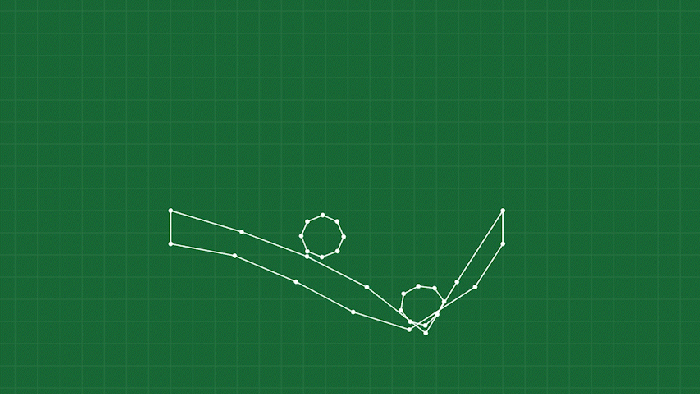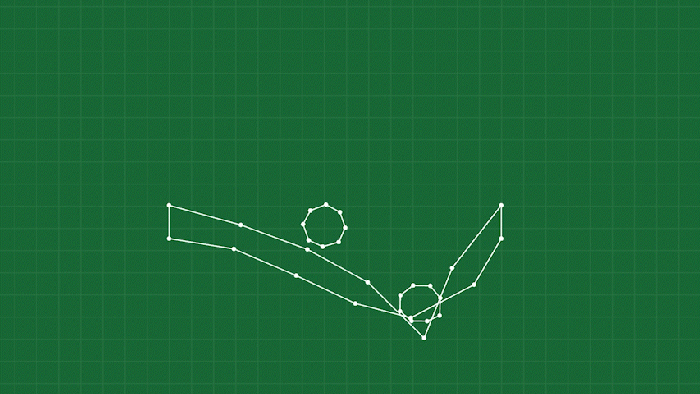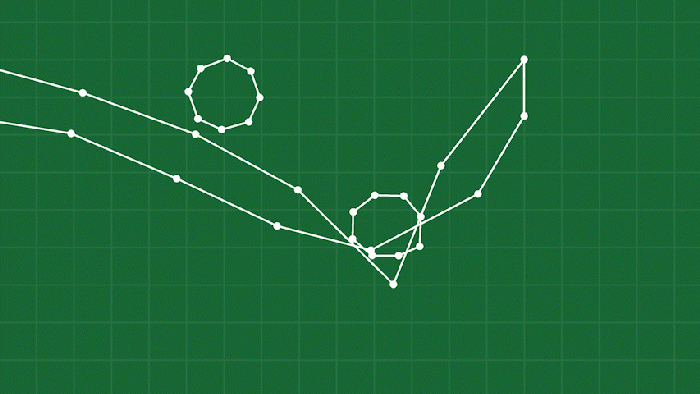
When a point is compressed hard enough, the springs have a tendency to “pop” to a stable configuration with the point on the wrong side of the object. You can of course just try to avoid this happening by not letting objects compress that much, but we are making a soft-body game after all, we want things to SQUISH.

My main solution to this is what I’m calling:

Shape Matching

The basic idea is this: what if we could have some spring forces that know the shape of the object, and always tried to pull on the points to get them back to the original shape? My solution works by imagining that the original shape of the object exists as a solid metal frame. Each physics step, we try to align the frame over the actual physics object, matching its position and angle as accurately as we can. Then, we can apply a spring force between each point on the object, and its corresponding point on this virtual rigid “frame.” These springs will always “pull” the points back toward their correct position:

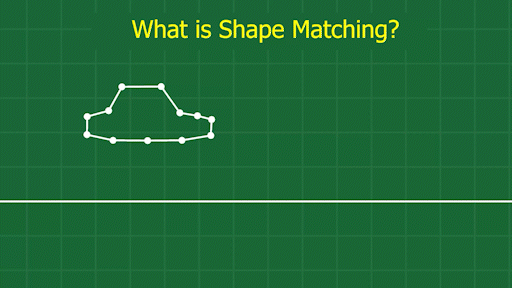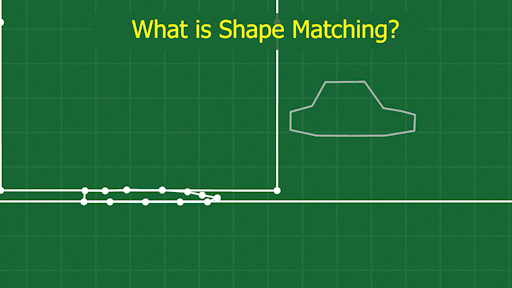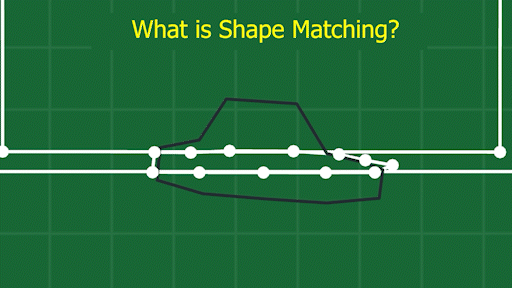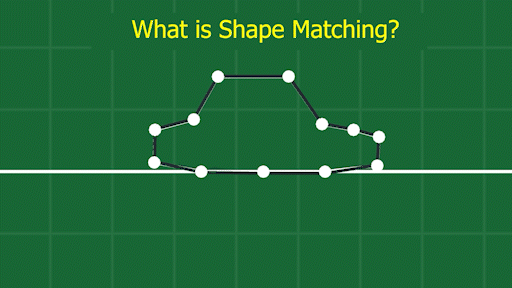
The trickiest part is figuring out where to place the frame. Since our objects are made up of many individually moving points, and likely deforming wildly, we don’t actually have a “position” and “angle” for the body as a whole. So, we have to derive it somehow. My method is pretty simple. First, average the positions of all the points involved to get the “geometric center” of the object. This is our position. Then, compare the angle from this center to each point, to the angle of the same point on the frame. Averaging these angles will give us an approximate angle for the body, based on where all the points are at the given moment. You can see this visualized here:

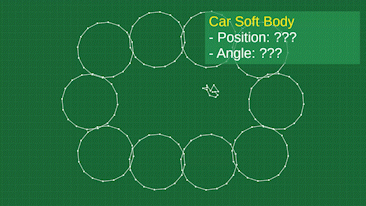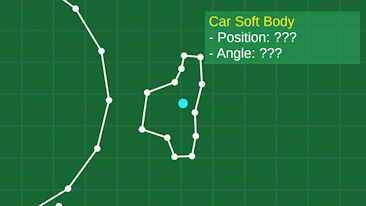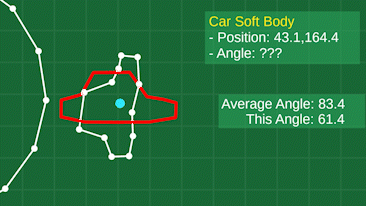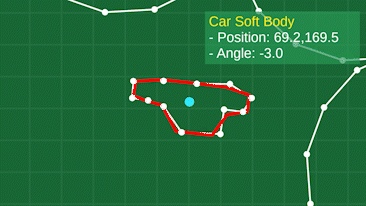
Shape matching makes a big difference, and allows for fun gameplay like the JellyCar getting completely squashed flat by a big heavy door, and it can pop back to its shape with ease.

This method does have a few things to watch out for. When an object is long and skinny, squishing it from one direction doesn’t displace the points as much as squishing it from the other.

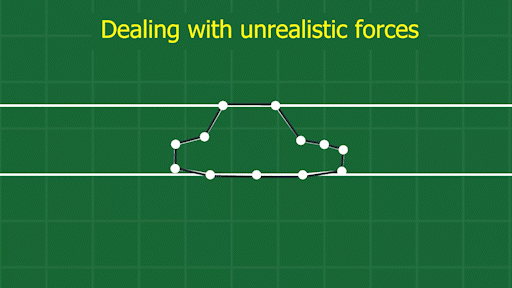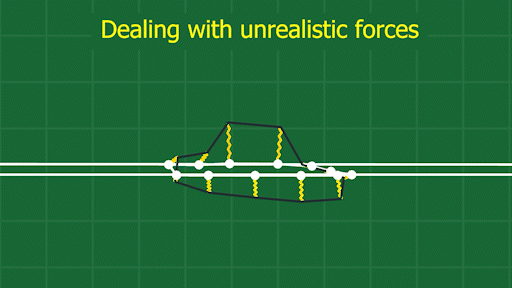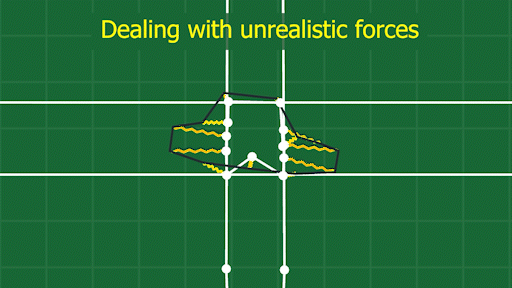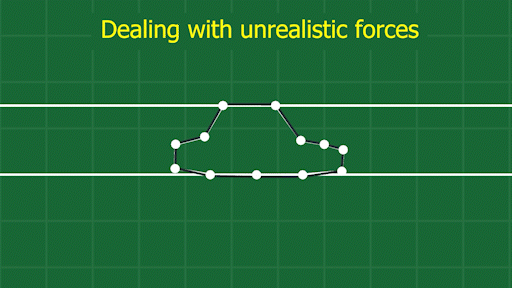
See how the points on the front and back of the car get pulled so far from the frame? This can produce unrealistically big forces that cause objects to behave unnaturally. I’ve overcome this by supporting multiple shape matching “frames” per object, so I can break up the frames into more localized areas of an object.

Note: while writing this article I also realized I could just clamp the force / max distance for the shape matching springs and that should help a lot! Hang on a second while I update my physics engine (lol).

Gas Giants

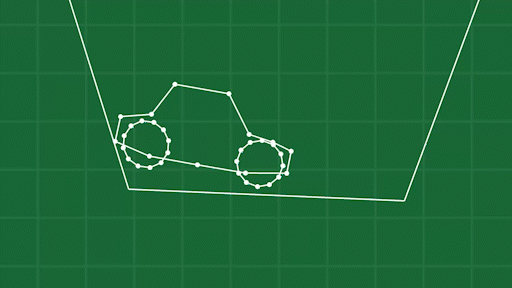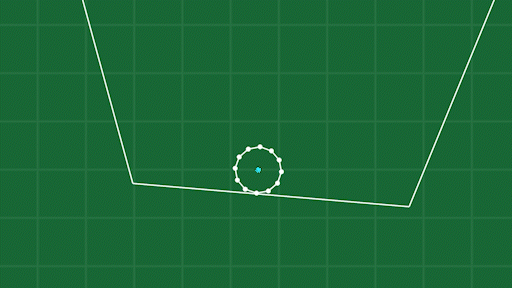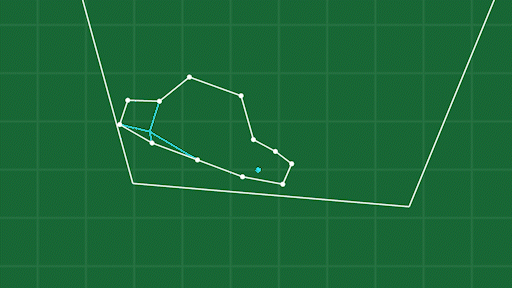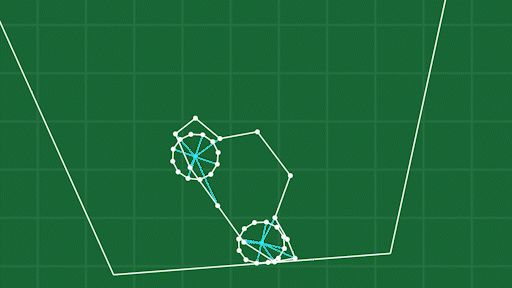
Another method that helps objects keep their shape is to fill them with virtual “gas” (like inflating a balloon.) This produces a pressure force pushing out on the edges of the shape, based on the volume of the object compared to the amount of virtual “gas” inside. This works amazing, and produces really great motion for objects. The tires on the JellyCar work like this, along with (pretty obviously) the balloon power-up.

The major downside to a pressure force is that it will always sort of push objects to become round/inflated. For example, using pressure on the car doesn’t help too much because it will distort the shape of the car:

Connecting Things Together

At this point we have described most of what we need to make a game like JellyCar! Except for a way to actually connect the tires to the car!

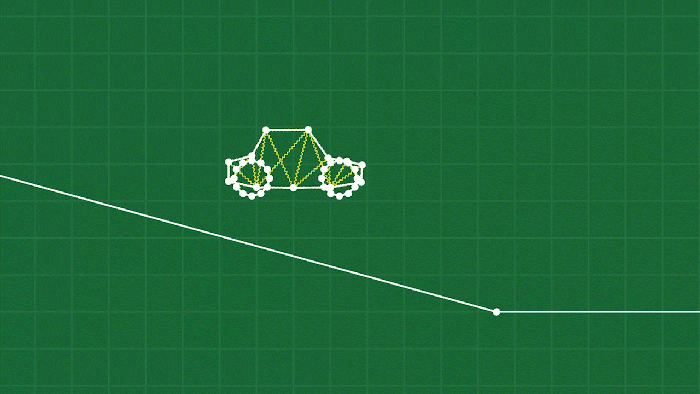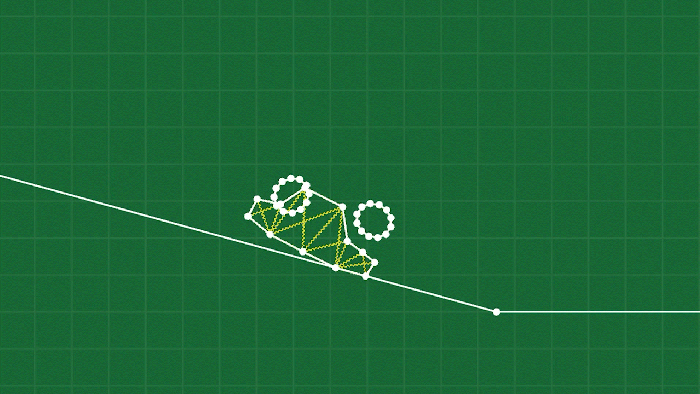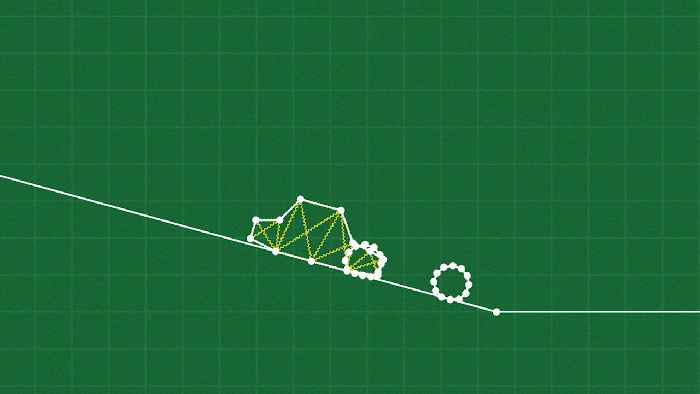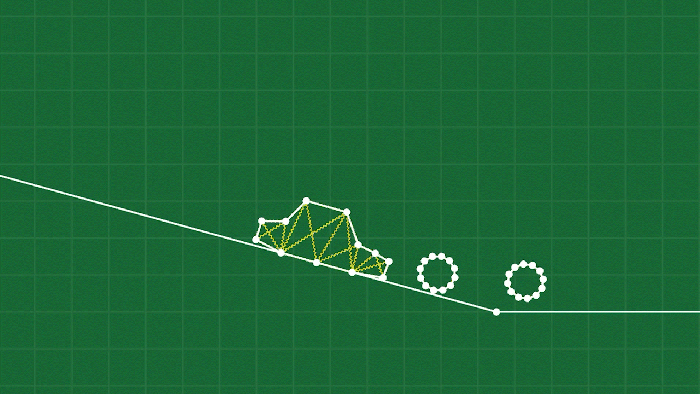
The final piece of the puzzle is the concept of joints. The simplest form of a joint simply “welds” two point masses together (presumably on different soft body objects) to connect them like a hinge. You can see this used a lot in the game, and it’s really just as simple as ensuring that the position of the two point masses are always identical (and possibly adjusting the velocities as well, depending on what sort of integrator you are using).

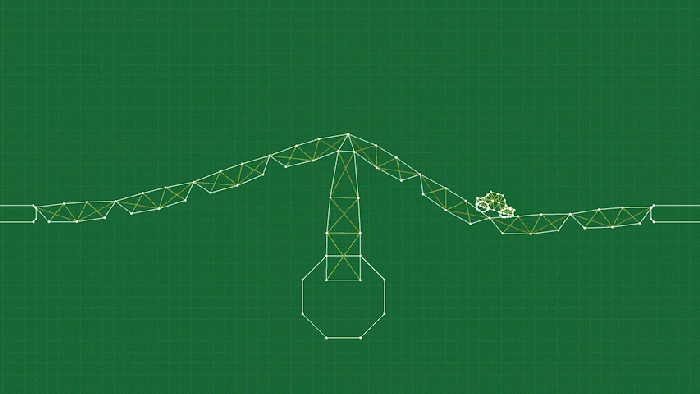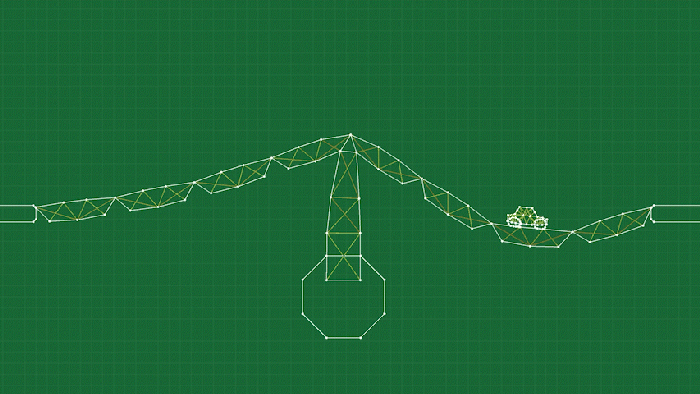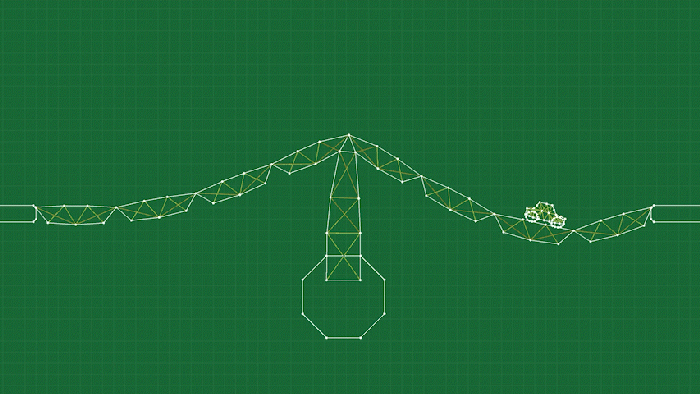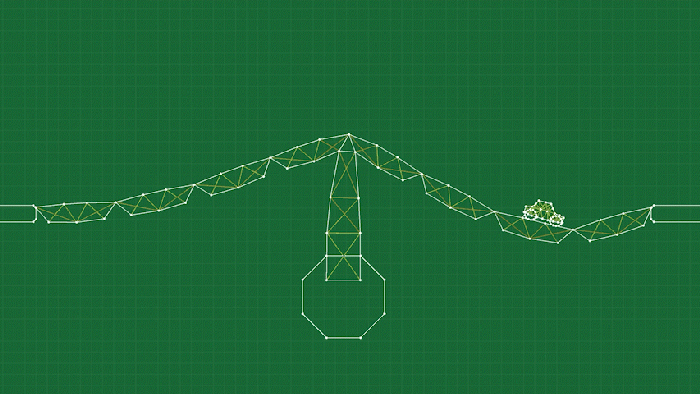
This doesn’t really work for attaching the tires to the car, though, because the two bodies don’t have conveniently placed point masses exactly where we need to connect them. For this I’ve made a slightly more complicated hinge that I call a “pin joint”. It works by selecting multiple points on a body, and creating an “anchor” through a weighted average of those points (after all, each point is moving independently on a deforming object.) Then we can do a similar procedure to the simple weld joint to make sure the two anchors stay connected, by moving (and adjusting the velocities) the points involved on each body to align the anchors.

That’s a Wrap!

OK, if you made it this far, you must be interested in physics simulations, thanks for reading to the end! I hope this has given you at the very least a better idea of how JellyCar works, and even perhaps inspired you to make some of your own custom physics simulations for yourself.