Global path planning in unknown and changing environments

This algorithm has been idling for a while now, and it's about time I shared this with the world. This is the non-academic version of my thesis (which has been fridged for nearly two years now). It focuses on finding a natural path in a (partially) unknown environment. I believe this may be an interesting approach for Real-time Strategy games using Fog of War.

There are many path planning algorithms around, but most of them deal with complete knowledge of the environment or act only for the moment, with no memory of what is behind them. Some algorithms like potential fields will get you trapped within local minima and attempt to break free of it artificially with random movements. As a result, all these algorithms will result in unrealistic behaviour. This algorithm aims to be to different.

A few starting notes
1) This is a global path planning algorithm, and it does not deal with local collision (unit) avoidance. That is beyond the scope of this post.
2) Like for every other algorithm that is and will be, this one is not a perfect for everything, but it deals with weaknesses that other some algorithms have.
3) It is meant for 2D gameplay , but it should be translatable to higher dimensions.

The basic A*
Anyone who has tried to implement path planning at least once, will know of A*. In short, it uses heuristics to rate and order nodes by shortest distance/lowest cost in a queue. It pops the first node in the queue, looks at its unvisited neighbours, rates them and adds them to the queue. This continues until a path is found, if one exists.

A* is typically used on a grid, subdividing an area into squares or hexagons. The problem here is environments in a RTS can become quite large, and the size of a square has to be small enough in order not to let the environments seem like a grid. On top of that, some RTS games allow the player to place buildings under any angle, resulting in partially filled squares which require extra thought. Still, it is an interesting algorithm because it will always find a path if one exists, and it's fairly efficient on itself.

The solution, part 1
Rather than using the environment as nodes for A*, you use the obstacles. Every obstacle keeps track of its corners and A* will be using these corners as nodes. These nodes are called permanent waypoints.

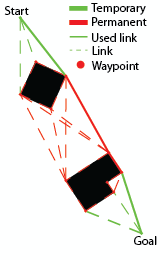
A simple case

The neighbours of a node, called links, are the other nodes that are in Line of Sight (LoS) with the node. The node's neighbouring corners are considered to be in LoS. Finding these links will be the most expensive part of this algorithm, but more on that later.
Your starting and goal nodes will be the unit and the target position, both finding and storing neighbours like the other nodes. These are temporary waypoints.

Right now we have acquired two advantages over the typical A* use. 
1) Instead of a Manhattan-like shortest paths, we really do get the shortest path available.
2) As long as the total of corners on our obstacles is less than the amount of gridspaces we would have had, we have a smaller search space. This is the case is pretty much every RTS I've played myself.


Howdy neighbour!
Finding the links of a node can be done in different ways (e.g. brute force, rotational plane sweep), but will always be relatively expensive compared to a gridbased version. Luckily this does not present a large problem, because it doesn't have to happen often. In a static environment, finding the links can all be done by pre-computation. For us this means that before the game starts, we can find all the links for all the obstacles that will be there at the start. Environments in a RTS rarely are static however, because often buildings can be built and destroyed. But only when this happens, we will have to update the links of our permanent waypoints. 

Note that you only have to recompute paths when we have had to update links as well.

The solution, part 2
I promised this would work for (partially) unknown environments. Well, we already have all the pieces for that. Rather than finding links for all the obstacles in the game, we only do this for those within our Field of View (FoV). This FoV is typically the combined LoS of all our units and buildings. Anytime a new obstacle comes in our FoV, we treat it like we do with new buildings; we update the links and paths. The same goes for obstacles that were in our FoV, left our FoV and got destroyed. They will not be updated until their location enters our FoV again. 

The solution, part 3
What do we do with large obstacles that are partially in our FoV? Once again we have options to choose from. The easiest, but less natural way is to simply pretend we know all about this obstacle now. The other option is to only add the permanent waypoints we actually see, and place temporary waypoints on the intersection between the Fog of War and our FoV. This will result in more natural behaviour but is also a lot more costly.

Cutting corners
So now we have a shortest path algorithm, based on the obstacles that we know of. Right now we will want to do a few things to polish this. Most importantly, the waypoints will now direct units through their walls. There are several ways to deal with this. The easiest way is to pretend the obstacles are a bit larger than they really are and that the nodes' waypoints lie outside of the actual obstacle.
Another way to do this, is to use a guide that moves over the path who steers the unit with and attraction force. When nearby obstacles cause a repulsing force when the unit you will not only avoid crashing into obstacles, but also create a smooth path for the unit, curving around the corners. This is often used to smoothen paths and is essentially a local potential field method.

The main advantages we now have are:
Natural behaviour within Fog of War systems
Very efficient in environments with large open space

Current drawbacks:
It doesn't instantly work for round shapes; they have to be sampled to a polygon.
Doesn't work out of the box with 'patches' that affect an unit's speed.

If you really want to get technical
Because we are doing this real-time, the algorithm's performance must be kept in mind. Suppose an environment has n regular polygonal obstacles with m corners on each obstacle. A permanent waypoint can be connected to up to (m/2 +1) other waypoints on another single obstacle it can link. The amount of singular links in between obstacles can be up to (n(n-1)/2), creating up to (n(n-1)/2) * (m/2 +1)  links between permanent waypoints, plus n for the links on the obstacles' borders. This yields us O(mn²) permanent links.

If we want to reduce this we can enforce a maximum number of links by only allowing obstacles to link the k-nearest obstacles, or dismiss links above a certain length. Another way to reduce the number of links is to use a visibility graph, which is a subset of our connected component.
It may also be interesting to group up bunched things like trees into forests and create a single obstacle boundary.


So there it is
Hopefully, this post will bring an end to the cheating those all-knowing units have done in the past. All jokes aside, it's been something that has kept me busy for a long time, and I hope it'll be to someone's advantage. Thanks for reading!