Sponsored Feature: Multi-Core Simulation of Soft-Body Characters Using Cloth

[In this Intel-sponsored feature, part of the Visual Computing microsite, Intel senior software engineer Brad Werth explains how multicore CPUs can be leveraged for an efficient method of representing soft-body characters by way of cloth simulation.]

Soft-body physics is an increasingly popular feature in videogames. Due to their computational intensity, soft-body physics are presently used sparingly to depict the movement of cloth, hair, and other flexible elements. This article shows how, with the additional processing power of a multi-core CPU, entire soft-body characters can be created using cloth simulation techniques.

This article draws heavily from a tech demo called Pet Me. The source to the Pet Me demo is available at http://www.intelsoftwaregraphics.com/?lid=2092&siteid=12. There is also a presentation based on this material hosted by Intel at http://software.intel.com/file/6712, and an explanatory video by the author at http://software.intel.com/en-us/videos/gdc-session-pamper-your-pets-with-cpu-power.

Most character animation is done today with a bones-and-skin method. This is sometimes called "skinning" a character. The basic idea is that the motion of the figure is controlled by a small number of invisible control points, linked together as bones. The visible portions of the character are then bound to specific bones. There is some cleanup work done to make joints look correct, or to blend between canned animations, etc. This method has been a favorite for a number of years, because it was a relatively fast way to animate characters given the constraint of a CPU with little computational power to spare. That constraint is rapidly becoming irrelevant with the advent of two-core and four-core processors. With the constraint removed, more sophisticated character animation techniques are possible.

With additional processing power, the bones-and-skin method can be extended for more detailed animation. More bones can be added for additional degrees of freedom. But there is no need to create additional bones unless a new joint is being modeled. Improvements are also possible by focusing on more complicated movement of the bones. Instead of just blending between canned animations, animations can be blended with physics to create dynamic motion in the bones. This is already implemented in games that use "rag doll" corpses, and has been implemented in some middleware products also.

Bones-and-skin is one method for character animation, but it is not the only viable choice assuming that increased computational power is available. Since the skin is the only visible part of the character, an alternative is to ignore bones and calculate the shape and movement of the skin directly. If the skin is disengaged from bones, then only local forces and constraints maintain the character's form. The resulting skin can be manipulated equally well from internal and external forces. A character built this way is sometimes called a "soft-body" character.

In a soft-body character, simulated cloth can be used as a skin. Forces applied to the cloth create the form of the soft-body character. Sock puppets are a simple example of this technique. The cloth provides local constraints to maintain the form of the sock, and the hand provides the forces to give the character volume. When simulating cloth computationally, the hand becomes an invisible mathematical construct and the sock is attached to that construct at key points. By expanding on this concept, a variety of soft-body characters can be created.

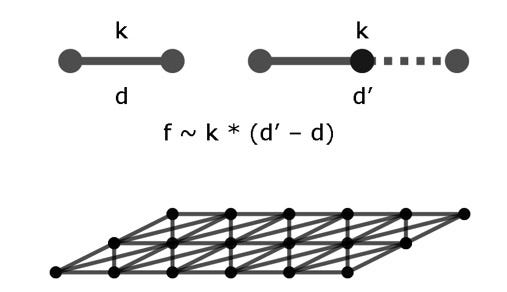
Figure 1: Using springs to model cloth

Cloth simulation is a well-known problem in computing. Figure 1 shows how cloth is commonly modeled as distinct points ("nodes") joined by springs. The physical definition of the spring force is calculated from the resting length of the spring, the stretched (or compressed) length of the spring, and a tension constant that defines how strong the spring is. As the equation shows, the force is proportional to the tension constant multiplied by the difference between the current length and the resting length. By arranging groups of nodes and springs, a coherent mesh is created - a cloth.

Figure 2: Cloth draped over a sphere

Here's the classic cloth demonstration showing a flat piece of cloth falling over an invisible sphere. These images were taken partway through the fall. In the wireframe image, the stretching of the center portion of the cloth is clearly visible. Cloth can be draped over any type of shape; the sphere is used here because of its mathematical simplicity.

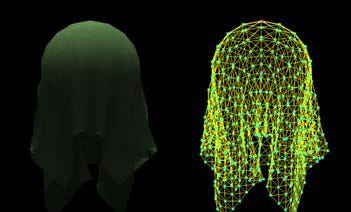
Figure 3: A ghost created by a classic cloth draped over a sphere

Even something as simple as a draped cloth can start to make an interesting character animation. Figure 3 shows a ghost created by draping a cloth over a sphere. The cloth drapes and flows around this sphere in a satisfying way. When moving, it looks something like a ghost. This is just a start, but it's encouraging that even the basics are already showing some promise.

Another interesting force to model on cloth is torsion. Torsion is like a spring that resists bending. This is intuitively present in many real-life cloth objects. A piece of paper is different from a handkerchief, in part, due to resistance to torsion. Clearly both objects resist stretching, but the handkerchief is easy to wad up into a ball, whereas the paper resists folding and attempts to remain flat. This can be modeled mathematically.

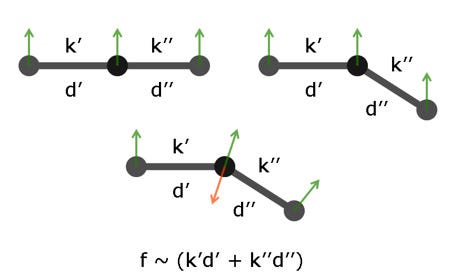
Figure 4: Torsion forces and normals on three connected points

Figure 4 shows the torsion force calculation for three points in a line. In the upper left diagram, the connection on the left half has a resting length d' and a torsion constant k'. The other half has length d'' and torsion k''. All points also have an identifying normal, pointing in an arbitrary, but consistent, direction. The diagram at the top right shows an intermediate state where the rightmost point has been moved relative to the other two points. Torsion forces are what attempt to bring the three points back into relative alignment.

In the bottom diagram for Figure 4, the normals have been recalculated for each point, where the left and right points have a local view of the outward pointing direction. The center node's normal is an average of the other two. The torsion force on the center point is opposite this normal and is proportional to the sum of each side's torsion constant multiplied by the resting length (the lever arm). There are also torsion forces on the end points (not drawn), which are aligned with their normals. The effect of these forces is to bring the middle point back between the two end points, returning them to a co-linear formation, although the whole line will be angled slightly clockwise from the original state.

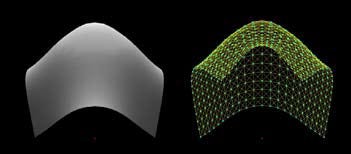
Figure 5: Cloth with moderate torsion draped over a sphere

With the addition of torsion, more interesting effects are possible with the classic cloth drop over an invisible sphere. Figure 5 shows the drop of a cloth where torsion has been increased to a moderate level and the cloth ends stand out in broad folds - like a rubber sheet. Torsion allows us to create some interesting effects in manipulation of cloth.

Figure 6: An ooze created with both tension and torsion forces

Figure 6 shows an ooze created with a cloth with both tension and torsion forces. The ooze is a square piece of cloth that has a central area of additional tension and torsion which elevates it above the ground. The torsion between the center of the ooze and the outside edges allows it to turn in a swirling motion to track a new target.

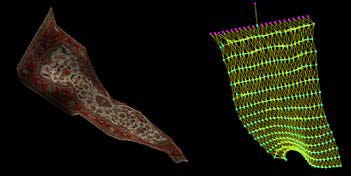
Figure 7: A flying carpet

Figure 7 shows a flying carpet. The carpet is truly a classic cloth used in a new way. The manipulation of the leading edge of the carpet, with the help of some moderate torsion forces, allows the carpet to twist and swoop in a compelling fashion. The wireframe view shows that this is just the classic cloth mesh, with the leading edge defined by a set of fixed co-linear points.

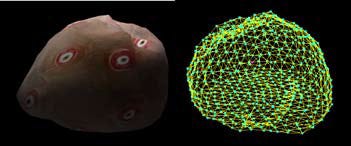
Figure 8: A squishy ball

Figure 8 shows a character made with cloth that is a subdivided icosahedron, with strong tension forces on the surface, but a very weak tension force in the center. The result is something like a collapsed soufflé, which rolls around due to the torsion applied by the center as it turns. Very cool but kind of disturbing, which is why the demo artist decided to texture it with eyeballs.

So far the math has been straightforward. But implementing just the tension and torsion forces alone will lead to cloth meshes that are very unstable. The two main problems are folding and oscillation. Folding occurs when the outside faces of the cloth mesh bend inwards on each other, and it can be solved reactively by doing a self-collision check within the mesh. Today, this is still prohibitively computationally expensive. Another solution is to proactively prevent folding by adding non-local connections with a moderate torsion constant. For example, the ooze has connections between its center point and all other points, which keeps the center from folding over the edge as it starts to move, and assists in turning the outside edges as the center turns.

Another approach is to introduce forces that reduce oscillation and prevent explosive oscillation. Damping is a mathematical application of a friction force, which prevents jittering and allows the cloth to eventually reach a rest state. Acceleration damping is an arbitrary, non-physical addition which prevents points in the mesh from rapidly changing direction. Rapid changes in velocity are usually a sign of a growing oscillation which will explode the mesh. Finally, rotation damping is another non-physical addition which acts a bit like the physical force of viscosity. Rotation damping is used to prevent torsion oscillations around the center of the mesh.

All this computation is a lot of work. To be clear, the calculation of forces and normals is conceptually simple - it's just the torsion and tension forces that were presented earlier. There is some significant math complexity involved and that is what the CPU labors over. But, since modern CPUs are now more capable, there are ways to prevent this computational effort from demolishing the frame rate of a game using even the most complex cloth simulations.

A multi-core CPU can do several calculations at once, by deploying multiple threads. Presuming that the main thread of a game has other work to do, the time-consuming calculation of forces and normals can be deferred for later computation by another thread. At the end of a frame, all the positions of the mesh points are available, and the forces for the next frame can be calculated immediately, based upon the time elapsed this frame. This works well assuming that the frame rate remains fairly steady. Since at the end of each update, the calculation of forces is deferred, the results must be "waited for" at the start of each frame. This "wait" can be defined such that if the forces are available, there is no delay, and if they are not, then the main thread will help compute the remaining parts.

In addition to deferring the calculation to another thread, the work can be broken into smaller pieces that can be processed by even more threads. This is useful on a four-core machine, for example. The Pet Me demo accomplishes this with a system built on top of the Intel® Threading Building Blocks. Intel® TBB is a cross-platform (Microsoft Windows*, Apple Mac OS X*, Linux*, and Microsoft Xbox 360*) Open Source library which implements a very efficient and scalable thread pool, and provides a useful API for dividing up computation between threads.

Figure 9: Code that demonstrates Intel® Threading Building Blocks usage to simulate cloth

Figure 9 shows code for a class that structures the forces calculation using Intel TBB. The calculation happens within the ConnectionForcesContext function operator(). The calculation object is passed indices of an array through this function, and then performs the desired calculation based upon what is found in that array. The array is the list of all the connections in the mesh, and the calculation object stores the forces that are applied to each point in the mesh, based upon the interaction of the connections.

The bottom half of the code in Figure 9 shows a snippet that invokes Intel TBB to perform the calculation. The parallel_reduce function is passed in a range object that specifies the size of the array, and is also passed in the calculation object that was defined earlier. Intel TBB will divide the range into pieces based upon a preferred number of elements in each chunk (the uGrainSize, above). Each time the range is divided, the copy constructor of the calculation object is invoked to maintain calculation state.

There is more information on Intel TBB at www.threadingbuildingblocks.org.

Figure 10: Intel® Thread Profiler visualization of the threaded cloth Calculation

Figure 10 shows the results of the threading effort as portrayed by Intel® Thread Profiler. The Intel Thread Profiler is a threading visualization and debugging tool that makes it straightforward to verify the effectiveness of a threading strategy. Each horizontal bar represents a thread, and a dark green area on a bar represents active computation being done by that thread. Thread sleep and blocking is represented by the pale green color. These screenshots were taken on a four-core processor.

Figure 10 shows a transitional point in the demo where the user has been running in a single-threaded mode, but has just switched to a multi-threaded mode. Initially, on the left side, one thread is doing all the computation. The active work is followed by an artificially added gap - this gap was intentionally introduced to the demo to represent the other computation typically performed by a game. The goal is to minimize the amount of time that the main thread is busy, and to ensure that the other threads are able to do useful work during this gap.

Figure 11: The fully parallelized calculation visualized in Intel Thread Profiler

Figure 11 shows that, after some initial work by the main thread, three other threads are becoming active. This is the defer-and-parallelize approach that was presented earlier. Threading Building Blocks has created three threads to accompany the main thread for a total of four threads on this four-core processor. The force calculation has been broken up into four equal pieces, and is being computed during the artificial gap introduced in the main thread. The work is divided into four pieces so that if the main thread completes its work before the computation on the other threads is done, the main thread can take on part of the computation, too.

Since users have a variety of hardware options, it is necessary to simplify the calculation for users with single-core CPUs. One method is to ignore the cloth forces and instead apply a simplified positioning of points in the mesh. Another option is to use a conventionally animated bone-and-skin model for users with single-core CPUs. Since both models will render the same number of triangles, users with multi-core CPUs get the full animation without significant impact to frame rate.

The demo of these techniques is a very simple one, and there are a number of improvements that could be made. Presently, the models in the demo are all defined mathematically - they are not output from a modeling tool in the conventional art pipeline. Thankfully, there are no real barriers to using a character modeling tool to output a soft-body character, since most of them already allow attaching of cloth to a bone-and-skin model. By putting the modeling emphasis on the cloth instead of the bones, a soft-body character can be created.

On a math note, many cloth simulations use a more optimized technique of simulation called Verlet integration. This technique makes some assumptions and uses some simplified math to allow the forces to be calculated more rapidly. Those assumptions and math work best when the framerate stays within a narrow band. Since this demo was designed to have wildly differing framerates (when switching between single-threaded and multi-threaded modes), the demo uses a very literal implementation of the underlying math. Games that use cloth-based characters are usually able to tune a Verlet integration for a targeted framerate and it will look right.

Soft-body physics have been used to good effect in many modern videogames. As appealing as the effects are, they have been limited to light use due to the computational intensity required. With an algorithm modified to take advantage of the computational power of multi-core CPUs, it is possible to simulate entire soft-body characters. A simple cloth simulation is straightforward to adapt in this fashion, and can be expanded to support the creation of expressive soft-body characters.