A few months ago, I was discussing with Adelaide, my wife, some ideas on games and their study. She isn't a gamer, although she is a good player and she enjoys some of the games in my collection. Her field is Linguistics, and much to her chagrin (she is too self-effacing) she is widely acknowledged as one of the leading linguists in Brazil (but don't ask me for details...).

Anyway, she has a sharp mind, and on this day, we were discussing the lack of a comprehensive, clear-cut definition of "game". She explained to me that Linguistics does not have such definitions for concepts such as "word" or "syllable", but this does not preclude their use. Furthermore, she told me of the distinctive feature system (DF), proposed by Trubetzkoy right before World War II, and developed by other linguists such as Jakobson, Halle and Chomsky. And she suggested that I investigated if such a system could be useful in Ludology.

Fast forward a few months, and her suggestion is now the centerpiece of my upcoming master's dissertation (to be presented in February, 2015). At the recent SBGames event, I presented a paper (co-written by my advisor and by Adelaide) describing the main points of a DF system in the study of games.

The paper was very well received, and it was selected as one of the three best full papers in the Art & Design papers track. It didn't receive first prize, but being one of the runners-up was already a nice distinction.

The paper is available on the site of SBGames 2014 Proceedings. The full text can be found at  http://www.sbgames.org/sbgames2014/files/papers/art_design/full/A&D_Full_Distinctive%20Features%20in%20Games.pdf, and its copyright is vested in SBC (the Brazilian Computing Society), which holds the publication rights. What follows are the main points of the paper.

Distinctive Features in Games

Authors: Luiz Cláudio S. Duarte, Dr. André Luiz Battaiola, Dr. Adelaide H. P. Silva

Institution: UFPR (Federal University of Paraná, Curitiba, Brazil)

Abstract

We propose a conceptual framework first used in phonology — the distinctive features (DFs) system — for the study of games. DFs represent key characteristics of a phenomenon. This enables a formal representation of characteristics of games, and can be used as one of the elements in a comprehensive, formal description of games. The DF system does not need a definition of “game”, even if such a definition can exist. It can be used to represent any artifact identified as a game. The system is flexible and extensible; a particular set of DFs can be tailored according to the needs of the researcher.

Introduction

“What is a game?” is a notoriously difficult question. Wittgenstein famously stated that “game” is not a definable concept, but rather a set of entities that share some “family resemblances” [Wittgenstein [1953] 2009, §66ff.].

This statement has not deterred many authors, who have offered several definitions of “game” [Juul 2003]. Sometimes the antagonism with Wittgenstein’s assertion is quite explicit, even acerbic, as can be seen in Thomas Hurka’s preface to the 2005 edition of The Grasshopper: Games, Life, and Utopia:

But in giving necessary and sufficient conditions for playing a game [Suits]’s doing exactly what Wittgenstein says can’t be done, and doing it about Wittgenstein’s own example. His book is therefore a precisely placed boot in Wittgenstein’s balls.

[Suits [1978] 2005, p. 11]

However, even Suits’s definition, so lauded by Hurka, has been contested, for not only there are games which do not conform to it [Geras 2008; Waern 2012], but Suits also includes in his definition some activities that are not considered games in common parlance (such as mountaineering).

Even more recent attempts at defining “game” have not reached quite all entities that are called “games” in common parlance. For instance, Juul [2003] proposes what he calls “the classic game model”, but his model excludes role-playing games (according to his view, “pen and paper role-playing games are not normal games”).

The search for a comprehensive definition of “game” may be misguided. Actually, even before it is attempted, it must first be asked: what kind of definition is desirable?

Philosophy studies distinguish several kinds of definition [Anil Gupta 2012]. Among others, there are descriptive definitions — that is, definitions that spell out meaning, and also aim to adequate themselves to existing usage — and stipulative definitions — which impart a meaning to the defined term for practical purposes, with no pretension of agreeing with prior uses of the term.

Perhaps Wittgenstein is right and a descriptive definition of “game” is unattainable. Even so, many of the proposed definitions, like Juul’s classic game model, are very useful stipulative definitions.

The search for a descriptive definition of “game” is not an idle quest. There is a very real need for a common, formal vocabulary about games — a critical language, as Costikyan [1994] put it. This would constitute an ontology, in the sense used by information and computer science: a body of formally represented knowledge, based on a conceptualization, which is used for knowledge sharing [Gruber 1995]. The ontology concept is much more complex in philosophy, but these other senses of the word are not relevant to this paper.

Besides many attempts to define “game”, there have been some attempts to define game ontologies, such as the Game Ontology Project (GOP), born out of José P. Zagal’s studies [Zagal et al. 2005]. The GOP presents a set of high-level concepts, such as “interface” or “rules”. Other concepts, such as “randomness”, are arranged in a hierarchical fashion, creating a tree.

Although hierarchies of concepts — or taxonomies — are easy to understand, they are not the only possible ontological framework applicable to the study of games. This has led to alternate proposals, such as Lindley’s orthogonal taxonomies [Lindley 2003].

In fact, although both definitions and taxonomies are very useful tools, there are alternatives for the creation of an ontology.

Ontologies are often equated with taxonomic hierarchies of classes, but [sic] class definitions, and the subsumption relation, but ontologies need not be limited to these forms. Ontologies are also not limited to conservative definitions, that is, definitions in the traditional logic sense that only introduce terminology and do not add any knowledge about the world…

[Gruber 1995, footnote 1]

Other fields of science also have to deal with “fuzzy” concepts, such as “word” or “syllable” in phonology. And the lack of clear-cut, comprehensive definitions for these concepts does not preclude their use, or the study of these concepts.

The reference to phonology in the previous paragraph is not an idle one. Phonological studies make use of an alternative ontologic framework that may be useful in the field of game studies. This framework is based on distinctive features (DFs).

In this paper, we propose the use of DFs as the foundation for an ontologic framework for the study of games.

Distinctive Features

In phonology, distinctive features (DFs) are the minimal units of the sounds of human speech, generally associated with specific articulatory or acoustic properties of sound [Hume-O’Haire and Winters 2006]. The study of DFs was pioneered in the work of Nikolai S. Trubetzkoy before World War II, and was developed by Roman Jakobson in the following years. DFs served as one of the foundations of Noam Chomsky’s influential studies of linguistics.

In its simplest form, DFs are a lexicon of categories, created in order to represent the relevant characteristics of a phenomenon. Each lexical entry further represents a binary feature of the phenomenon ([±]), which may be present [+] or absent [–]. For instance, in a DF lexicon which included the entries [±animate, ±human, ±feminine], the concept cow could be represented by [+animate, –human, +feminine] [Chomsky and Halle 1968, p. 295].

One crucial aspect of a DF system is the determination of its features set — that is, the enumeration of its lexical entries.

Indeed, the system features must not be arbitrarily chosen, but they must be determined according to the characteristics of the phenomenon that are relevant to the researcher [Chomsky and Halle 1968, p. 295]. In the case of human language, these features derive from articulatory and acoustic properties of the speech, or from characteristics of gestures, in the case of sign language [Lane, Boyes-Braem, and Bellugi 1976].

Phonologists have determined that speech is a complex phenomenon, but DFs offer a consistent representation for it. As such, it allows the effective sharing of knowledge among linguists, and it thus constitutes the framework of an ontology.

Can the DF system be used in game studies? We believe that this is possible, as will be seen in the next section.

Creating Game DFs

We have stressed in the previous section that the features represented in a DF system must not be arbitrarily chosen. Rather, they must be determined according to the characteristics of the phenomenon that are relevant to the researcher.

In order to show how to create such a system, we present a simple exercise, as an example. We take on the roles of researchers interested in the media in which games exist.

The first results from our analysis distinguish digital games from non-digital games. This suggests the use of a DF, which we will define as [±digital]. This DF indicates whether a game is implemented in an electronic device (computer, console, mobile phone, it doesn’t matter) or not. In the first case, the game would be represented as [+digital]. In the second case, the game would be represented as [–digital].

Fig. 1: Tetris and Hopscotch

Thus, Tetris is represented by [+digital], and the children’s game Hopscotch is represented by [–digital] (fig. 1).

As we continue our example research, we find out that the border between digital and non-digital games is not clear-cut. For instance, Chess is an ancient non-digital boardgame; but it can be implemented in a computer, either as a virtual board for two human players to play against one another, or with a programmed artificial intelligence as one of the players (fig. 2).

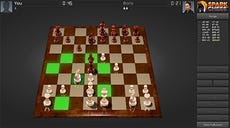
Fig. 2: A physical Chess board (left), and a digital implementation of this game (right).

Is Chess a digital game or a non-digital game?

Once again the fuzzy borders of the game universe create a conceptual problem. But actually the answer to this question depends on the answer to another question: are both games in fig. 2 the same?

Many games present variants, and Chess is foremost among them. There are many Chess variants, often created by scholars and master players, presenting a great many permutations between rules, boards, and pieces.

There are other games which are usually considered Chess variants, although they have not derived from purposefully-crafted changes to the classical game. Rather, they are the historical stages in the cultural process that originated modern Chess.

One of Chess’s ancestors is Chaturanga, played in the Gupta Empire in India around the 6th century AD. Another is Shatranj, which originated from Chaturanga, and which was played in Sassanid Persia around the same period. This game spread throughout the Muslim world, and, in the Middle Ages, reached Europe through Spain. There it changed into modern Chess.

Is Chaturanga a Chess variant? What about Shatranj? Or is Chess a variant from one or both of them?

There are no definite answers to questions like these. Just as in Wittgenstein’s previously mentioned statement on games, the variants of a game present a set of entities that share some “family resemblances” among them.

Any of the propositions about the Chess family of games can be right, depending on the purpose of the analysis, and depending on the relevance for the researcher of the degree of variation. Thus, a researcher of Chess’s emergent properties may consider Fischer’s game (where the starting positions of the noble Chess pieces are randomly determined) as a Chess variant, and Gliński’s game (which features an hexagonal board and hexagonal spaces) as a different game. On the other hand, a game history scholar may consider all of them as Chaturanga variants.

All of this lead back to the first question: is Chess a digital game? It can be argued that it should be [+digital], since it can be implemented in a computer. But, of course, a digital version of Chess can present some differences from the board game; for instance, a digital Chess can highlight the legal moves for a piece, and thus help in learning the game or in planning a move.

This conundrum may be solved by stating an axiom for any DF-based framework.

Axiom 1. A set of DFs may characterize one particular instance of a game, but not necessarily all instances of that game.

In other words, according to this axiom, some DFs of a game may vary from one of its implementations to another.

Thus, in this particular example framework — in which we are proposing to study games according to their media — it does not make any sense to ask whether Chess is a digital game or a non-digital game. Rather, this question must be asked for each particular implementation of Chess. In the case of the two instances of Chess pictured in fig. 2, the one on the left is thus [–digital] and the one on the right is [+digital]. We could say that we have two variants of the same game.

As a matter of fact, the Chess example highlights how to expand the medium-related example DFs framework, which thus far has only one feature, [±digital]. Chess is a boardgame, that is, a game which is played on a board. This is a portable version of the “magic circle”, a concept borrowed from Huizinga [[1938] 1949] and used as shorthand for the special place where the game takes place, and where the rules of the game take precedence over the rules of the “real” world [Salen and Zimmerman 2004, p. 95]. A board is not only the area where the game takes place;, its different areas acquire a meaning which is imparted by the rules.

Some games have boards (Chess), and some games don’t have them (Poker). And this distinction is not confined to [–digital] games; there are several [+digital] games that feature virtual versions of boards, such as the digital Chess on fig. 2, and [+digital] games that don’t have boards, such as Doom.

This indicates that we can define another DF, namely [±board], which is independent of the [±digital] DF. The [±board] DF indicates whether the game uses a board as one of its elements.

This allows us to represent Doom as a [+digital, –board] game. The physical Chess game in fig. 2 is represented by [–digital, +board], and its digital sibling is represented by [+digital, +board].

Fig. 3: Poker being played on a kitchen table (left) and online (right).

A game without a board and which is not played on a computer would thus be represented as [–digital, –board]. This would be the case of Hopscotch, or of a Poker game played by friends over a kitchen table; the table isn’t a board, but merely a convenient surface used to accomodate the game elements. On the other hand, a Poker game played in an online casino could be represented as [+digital, –board] (fig. 3).

This simple exercise showcases the strengths of the DF framework. It was not necessary to define what we mean by “game”. Perhaps there is a definition of “game” that includes games as varied as Hopscotch, Tetris, Doom, Poker and Chess. But we do not need it. It is even possible, for instance, that some people do not consider Hopscotch a “real” game, but this does not preclude its representation in this system as [–digital, –board] — and to actually discuss whether it is a game or not becomes a moot point.

On the other hand, this same exercise highlights one problem with the DF framework. We started with a single DF, and then refined the granularity of the framework by adding another DF. With one binary DF we had 2 categories of games, and when we added another DF we then had 4 (or 2²) categories. The first two categories were thus broader than the four latter ones.

Are these categories enough? Perhaps we could introduce a [±cards] DF, which would represent games that feature cards (either common playing cards or custom-made cards) as [+cards] and other games as [–cards]. Thus, the kitchen-table Poker would be represented as [–digital, –board, +cards], Doom would be represented as [+digital, –board, –cards], and so on. We would have now 8 categories (2³).

The key decision here is where to stop “zooming in”. Once again, this depends on the intentions of the researcher: specifically, what are the features that are relevant to the investigation?

It is theoretically possible to pile up DFs upon DFs until we could differentiate Monopoly: Star Wars from Monopoly: Pokémon — but this would only make sense if such differentiation would be meaningful in the context of the research being developed. If the DF system was being developed for an analysis of the media of games, for instance, it would be absurd to include a DF which could differentiate between these two versions of Monopoly.

Thus, the chosen DFs must depend on what is being studied. But there is another necessary condition for a coherent set of DFs: the chosen DFs must be independent from each other.

For instance, we can define [±p] and [±q] as DFs in our system. But then we find that every instance of our universe of games is either [+p, +q] or [−p, −q], and this reveals that both [±p] and [±q] represent the same characteristic. Thus, one of them is superfluous.

Final Thoughts

We started this investigation with a reference to phonological studies. The sounds of human speech are limited by the physics of sound and by the biological constraints of the phonatory system. But even this limited set of sounds can be described by several DFs, and there is considerable debate as to the best set of DFs that will describe these phenomena.

Games, on the other hand, offer an almost boundless experience. Games are as diverse as the humanity that created them. This diversity means that trying to sort games in definite, discrete categories is as fruitless a task as trying to empty the ocean with a bucket.

But the use of a DF-based system bypasses this difficulty. With an adequate set of DFs, it is possible for a researcher to state that his analysis pertains, for instance, only to [+digital, –board] games.

Perhaps in the future a set of “game” DFs can be proposed, covering all games in existence according to some definition. Inevitably, there will be games which will push the borders of this definition. However, since the DF system is extensible, it will be possible to amend the proposed set, to include a new DF, for instance, covering the “new” games.

This is a novel approach for ludology. The strengths of the proposed DF system are its inherent flexibility and extensibility. The DF system can be used in the study of all games.

We do not need a definition of “game”. And thus we have no need to kick Wittgenstein’s balls.

References

Chomsky, Noam and Halle, Morris (1968). The Sound Pattern of English. New York: Harper & Row.

Costikyan, Greg (1994). “I Have No Words & I Must Design”. In: Interactive Fantasy, page 22.

Geras, Norman (2008). Games in Progress. URL: http://normblog.typepad.com/normblog/2008/04/games-in-progre.html (visited on May 6, 2014).

Gruber, Thomas R. (1995). “Toward Principles for the Design of Ontologies Used for Knowledge Sharing”. In: International Journal Human-Computer Studies. Volume 43, issues 4–5, pages 907–928.

Gupta, Anil (2012). “Definitions”. In: The Stanford Encyclopedia of Philosophy. Edited by Edward N. Zalta. Fall 2012.

Huizinga, Johan ([1938] 1949). Homo Ludens: a study of the play-element in culture. London: Routledge & Kegan Paul.

Hume-O’Haire, Elizabeth and Winters, Stephen (2006). “Distinctive Feature Theory”. In: Encyclopedia of Cognitive Science. URL: http://onlinelibrary.wiley.com/doi/10.1002/0470018860.s00242/abstract (visited on May 8, 2014).

Juul, Jesper (2003). “The Game, the Player, the World: Looking for a Heart of Gameness”. In: Level Up: Digital Games Research Conference Proceedings. Utrecht, pages 30–45.

Lane, Harlan, Boyes-Braem, Penny, and Bellugi, Ursula (1976). “Preliminaries to a distinctive feature analysis of handshapes in American Sign Language”. In: Cognitive Psychology 8.2, pages 263–289.

Lindley, Craig (2003). Game Taxonomies: A High Level Framework for Game Analysis and Design. URL: http://www.gamasutra.com/view/feature/131205/game_taxonomies_a_high_level_.php (visited on May 7, 2014).

Salen, Katie and Zimmerman, Eric (2004). Rules of Play: Game Design Fundamentals. Cambridge (MA): The MIT Press.

Suits, Bernard ([1978] 2005). The Grasshopper: Games, Life, and Utopia. Peterborough: Broadview Encore Editions.

Waern, Annika (2012). Bernard Suits’ “The Grasshopper”. URL: http://annikawaern.wordpress.com/2012/03/08/bernarn-suits-the-grasshopper/ (visited on May 6, 2014).

Wittgenstein, Ludwig ([1953] 2009). Philosophical Investigations. 4th edition. Translated by G. E. M. Anscombe, P. M. S. Hacker and Joachim Schulte. Chichester: Blackwell Publishing.

Zagal, José P. et al. (2005). “Towards an Ontological Language for Game Analysis”. In: Proceedings of DiGRA 2005 Conference: Changing Views – Worlds in Play.

Image Credits

Fig. 1, left: Tetris screenshot.

Fig. 1, right: Hopscotch in California. Photo by Dave Parker. Available through Wikimedia Commons.

Fig. 2, left: Staunton Chess set. Photo by Lee Daniel Crocker. Available through Wikimedia Commons.

Fig. 2, right: Screenshot from http://www.sparkchess.com/.

Fig. 3, left: Poker at home. Photo by Jon Holt. Available through Flickr.

Fig. 3, right: Screenshot from Poker TH open-source software. Available through Wikipedia.